Семейство поверхностей, заданное формулами преобразования координат, и его огибающая

Аннотация

А.А. Ляшков, А.М. Завьялов

Дата поступления статьи: 31.01.2013

  Решается задача исследования особенностей отображения ортогональным проецированием гиперповерхности на гиперплоскость применительно к задачам профилирования режущего инструмента. Поставленная задача реализована на основе установленных закономерностей в расположении точек сечений гиперповерхности относительно координатных гиперплоскостей. Исходными данными являются двумерная поверхность и формулы преобразования координат, определяющие закон ее относительного перемещения. Гиперповерхность, образованная на основе такого семейства двумерных поверхностей, является объектом исследования.  Полученные результаты иллюстрируются двумя примерами.  

Ключевые слова: семейство поверхностей, гиперповерхность, профилирование, особенность отображения, режущий инструмент

05.01.01 - Инженерная геометрия и компьютерная графика

ФГБОУ ВПО «Омский государственный технический университет»

Введение
Вопросам исследования отображения ортогональным проецированием поверхности на плоскость посвящено значительное количество работ: [1, 2, 3, 4] и другие. В них, в основном, определяются некоторые дифференциальные характеристики очерка двумерной поверхности или алгебраической поверхности большей размерности.  Так в работе [3] предлагается определять точки контурной линии по уравнениям поверхности, заданным в неявной форме и уравнениям, содержащим дифференциальные характеристики этой поверхности. Для  расчета предлагается использовать методы вычислительной математики и методы нелинейного программирования. Что является не простой задачей. Анализа контурной линии и ее проекции не приводится.
Во многих прикладных задачах, связанных с профилированием режущего инструмента, определяют огибающую семейства поверхностей. Наряду с классическим подходом к определению огибающей в последнее время используется и новый. Так, если спроецировать график семейства двумерных поверхностей в пространство R_4, то получим некоторую трехмерную гиперповерхность Σ. Криминанта этой поверхности является   огибающей рассматриваемого семейства. Исследование поверхности  Σ при задании ее параметрическими уравнениями и уравнением в неявной форме проведено в работах [5], [6].  Установлено ряд новых свойств такой поверхности. В связи с тем, что при профилировании режущего инструмента семейство поверхностей задается формулами преобразования координат [7], важной задачей является исследование полученной таким образом гиперповерхности.
Криминанта гиперповерхности
Пусть исходная поверхность задана в подвижной системе координат 0XYZ уравнением в неявной форме
   (1)
Эта поверхность совершает некоторое движение относительно неподвижной системы координат 0₁x₁y₁z₁. В общем виде формулы преобразования координат, выражающие x₁, y₁, z₁ через x, y, z , можно записать так
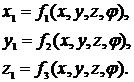   (2)
где  φ – параметр относительного движения.
Уравнения (1) и (2) определяют  семейство поверхностей в пространстве R₃. При проецировании графика этого семейства в пространство  R₄  будет получена гиперповерхность Σ в системе координат X₁Y₁Z₁Q₁ и заданная в виде
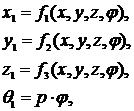          (3)
где р – некоторая константа.
Наложим на две координаты y₁ и z₁ условия связи
y₁=a, z₁=b,
где a и b – некоторые константы.
Тогда функция Лагранжа, позволяющая определить условный экстремум координаты x₁ , будет

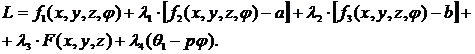
Соответствующая  система уравнений, из решения которой устанавливается связь параметров поверхности и параметра семейства, имеет вид





Рассматриваем последние три уравнения, с учетом l4=0, как систему неоднородных линейных уравнений относительно множителей Лагранжа. Из решения этой системы по формулам Крамера имеем
  
а соответствующие определители будут




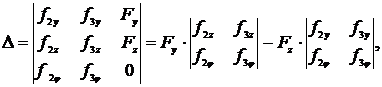
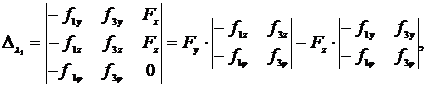
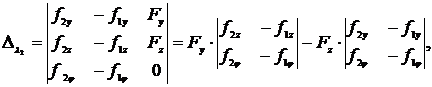
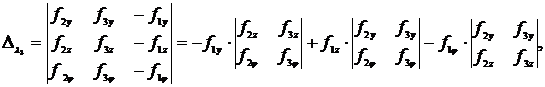
После подстановки полученных зависимостей в первое уравнение системы неоднородных линейных уравнений получим
(4)

Или после подстановок выражений из определителей

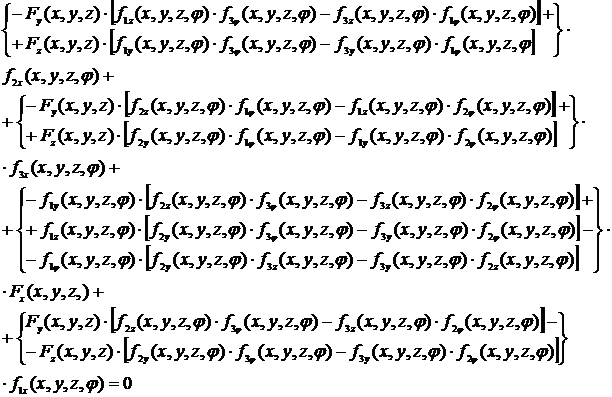
Полученное равенство устанавливает связь координат исходной поверхности и параметра φ их семейства. Тогда уравнения (4), (1) и (3) определяют дискриминанту гиперповерхности, а уравнения (4), (2), (3) – ее криминанту и, соответственно, огибающую рассматриваемого семейства поверхностей. 
Огибающая семейства сфер в их поступательном движении
В качестве примеров, иллюстрирующих достоверность полученных результатов, рассмотрим сферу, заданную в подвижной системе координат 0xyz уравнением
    (5)
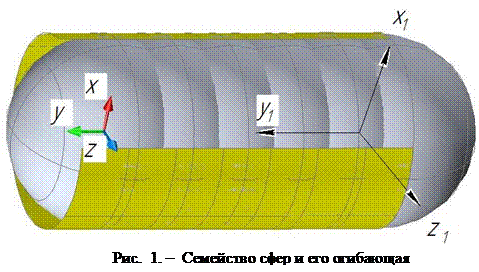
Эта сфера (пример 1) совершает поступательное перемещение вдоль оси y₁ (рис. 1) неподвижной системы координат, которое задается формулами преобразования координат
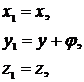   (6)
где φ – параметр движения.
Тогда входящие в равенство (4) определители будут
 
Подставив полученные выражения в (4), получим y=0.
Уравнения сферы и формул преобразования координат, в которых y=0, позволяют определить огибающую рассматриваемого семейства сфер в виде

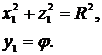
Эти уравнения определяют проецирующую относительно координатной плоскости X₁Z₁  цилиндрическую поверхность (рис. 1).

Огибающая семейства сфер в их винтовом движении
Пример 2. Пусть задана та же  сфера (5),  но  совершает она винтовое движение (рис. 2). Формулы преобразования координат, определяющие это движение, имеют вид

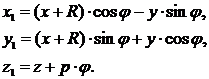              (7)

Уравнения (5) и (7) определяют  семейство поверхностей в пространстве R₃. График этого семейства в R₄ представляет собой гиперповерхность,  заданную  в системе координат X₁Y₁Z₁Q₁ , в виде
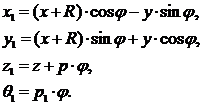    (8)
Для установления связи параметров поверхности и движения вычислим определители, входящие в уравнение (4)


  
Тогда уравнение связи параметров будет:  Откуда имеем
        (9)
Из уравнения сферы для p=0 (сфера совершает вращательное движение) следует: x₂+z₂=r₂ . Из первых двух уравнений системы (7) , а из трех уравнений этой системы получим 

После подстановок и преобразований получим уравнение
          (10)

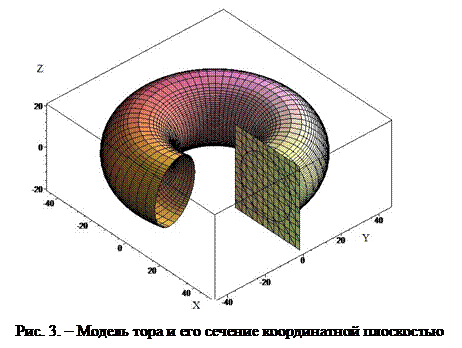
графиком которого является тор (рис. 3)

После подстановки выражения для y из (9) в уравнение сферы получим
.
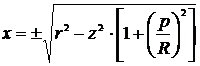Подставив выражения для x и y в уравнения (7) получим уравнения дискриминанты гиперповерхности (8)
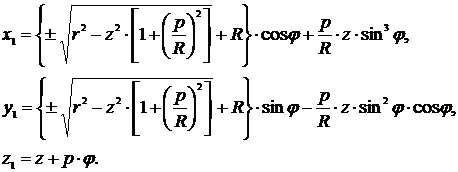               (11)  
Графиком полученных уравнений является трубчатая винтовая поверхность (рис. 4).

Для p=0  система (11) преобразуется к виду
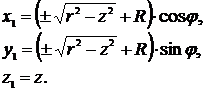        (12)  
Система уравнений (12) в параметрической форме определяет ту же поверхность тора, что и уравнение (10).
Поверхность (11)  может быть получена также винтовым движением окружности, расположенной в плоскости, перпендикулярной вектору касательной к винтовой линии (рис. 2). Уравнение винтовой линии, образованной движением точки O, будет

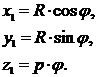
Касательная к винтовой линии определяется равенствами

Для φ=0 координаты касательного вектора  Из уравнения плоскости, , перпендикулярной этому вектору получим

Тогда уравнения поверхности, образованной винтовым движением окружности, будут

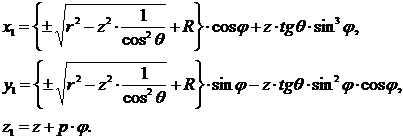
Последние уравнения, так же как и уравнения 11, определяют трубчатую винтовую поверхность (рис. 5).

Введя новый параметр  получим уравнение трубчатой винтовой поверхности в виде

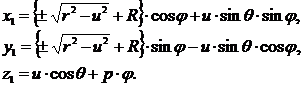
График трубчатой винтовой поверхности для новой параметризации представлен на рис. 6.

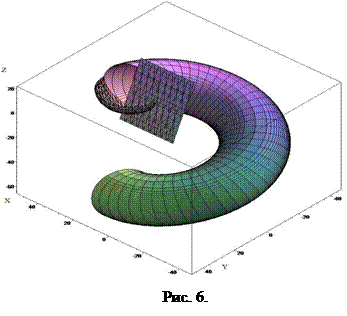
Таким образом, проведенные исследования, на основе полученных ранее результатов, гиперповерхности и ее отображения ортогональным проецированием на координатную гиперплоскость позволили получить в общем виде огибающую семейства двумерных поверхностей. Исходная поверхность задается уравнением в неявном виде, а семейство поверхностей определяется формулами преобразования координат.
Полученные результаты апробированы на двух примерах с получением как аналитических зависимостей так и соответствующих компьютерных полигональных моделей поверхностей, иллюстрирующих достоверность приведенных результатов.

Литература

1. Арнольд,  В. И. Особенности гладких отображений [Текст] / В. И. Арнольд  – Успехи мат. наук. – 1968. – т.XXIII, вып. 1(139). – С. 4–44.
2. Брус Дж.,  Джиблин П. Кривые и особенности [Текст]. / Дж., Брус,– М.: Мир, 1988. – 262 c.
3. Быков, В. И. Определение контурной линии на поверхности, заданной уравнением в неявной форме [Текст] // В сб.: Тезисы Всесоюзного научно-методического симпозиума “Применение систем автоматизированного проектирования конструкций в машиностроении”. – Ростов-на-Дону. –  1983 – С. 40–41.
4. Платонова, О. А. Проекции гладких поверхностей [Текст] / О. А. Платонова // Тр. Семинара им. И.Г. Петровского. – 1984. – т. 10. – С. 135-149.
5. Ляшков А. А., Волков В. Я., Отображение ортогональным проецированием гиперповерхности на гиперплоскость [Текст] //  Вестник Иркутского Государственного Технического Университета. – 2012. – № 2. – С. 18-22.
6. Ляшков, А. А. Отображение ортогональным проецированием поверхности, заданной параметрическими уравнениями /  А. А. Ляшков //  Омский научный вестник. – 2012. – № 2(110). – С. 9-13.
7. Лашнев С. И., Юликов М. И. Расчет и конструирование металлорежущих инструментов с применением ЭВМ [Текст] / М.:  Машиностроение, 1975.  – 392 с.