Трещиностойкость железобетонных элементов со скозными отвестиями при кручерии и при кручении с изгибом

Аннотация

С.Х. Байрамуков, С.С. Дюрменова

Дата поступления статьи: 27.02.2013

Рассматривается трещиностойкость железобетонных элементов со сквозными отверстиями. Сопоставление теоретических и опытных моментов трещинообразования при кручении  и при интенсивном кручении с изгибом. Предложена формула для практических расчетов трещиностойкости железобетонных элементов со скозными отверстиями при кручении и формула для оценки трещиностойкости железобетонных элементов со сквозными отверстиями при интенсивном кручении с изгибом.

Ключевые слова: трещина, изгиб, кручение, железобетон, элемент, отверстие, балка

Железобетон, как наиболее экономичный материал для строительных конструкций в обозримом будущем будет основным в практике строительства. Как известно стоимость железобетона определяется стоимостью входящих в его состав материалов, экономия которых является важнейшим источником снижения материалоемкости и стоимости конструкций [1].
На практике одним из путей экономии материалов является разработка и совершенствование методов расчета  [3,4,5], отвечающих наилучшим образом действительной работе конструкции. Отсутствие подобных методов при составлении нормативных документов приводит к принятию расчетных положений, заведомо предполагающих необоснованный запас прочности .
Способность железобетонных конструкций выполнять требуемые функции в течение длительного времени при эксплуатации в разных условиях определяет сочетание свойств арматуры и бетона [7].
Основным способом оценки состояния материала являются различные разрушающие методы – многочисленные испытания на растяжение, сжатие, изгиб и т.д. [2]. Разнообразие случаев разрушения и параметров, от которых зависят эти случаи, при их исследовании предполагает необходимость привлечения  как можно большого экспериментально-теоретического материала [9,10] .
Актуальность данной статьи обусловлена тем, что она посвящена совершенствованию методики расчета прочности железобетонных стержней сквозного сечения, подверженных кручению и изгибу с  кручением.
При исследовании трещиностойкости железобетонных элементов в основу была положена методика, разработанная Касаевым Д. Х. [6]. По этой методике теоретическое значение момента образования трещин опытной балки сплошного сечения определяется по формуле
,      (1)
- упругопластический момент сопротивления образца сплошного сечения; b и h – ширина и высота поперечного сечения балки соответственно.
Как будет вести себя балка со сквозным отверстием под действием крутящего момента неизвестно. Поэтому были осуществлены расчеты по трем вариантам:
первый вариант – расчет как сплошной балки по формуле (1);
второй вариант – расчет отдельно для каждой ветви балки с последующим удвоением результата, т. е. по формуле
,   (2)
где  момент сопротивления сечения ветви балки равен ;
b и d – высота и ширина сечения ветви соответственно;
третий вариант – расчет по формуле (1) за вычетом размеров отверстия, т. е. по формуле   
,     (3)
где;; ;;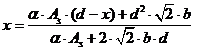;; d – высота сечения ветви; b - ширина сечения балки.
За основу принимается тот вариант расчета, в котором получена наилучшая сходимость результатов опыта и расчета.
Сопоставление результатов расчета по вариантам 1, 2 и 3 с опытными значениями приведено в табл. 1.
Таблица №1
Результаты сопоставления теоретических и опытных моментов образования трещин балок серии I при кручении

№  п/п	Шифр балки	b, см	h, см	d, см	R <ыги>bt , МПа	Wт.pl, см 3	, кНсм	, кНсм
1	2	3	4	5	6	7	8	9	10
Вариант 1
1.	БТ	15,0	22,0	11,1	1,825	2993	545	537	0,99
2.	БТ 30-0	14,8	22,0	11,1	1,942	2953	573	549	0,96
3.	БТ 60-0	15,0	21,8	11,0	1,726	2939	505	420	0,83
4.	БТ 90-0	15,1	21,9	11,0	1,706	2986	507	418	0,82
5.	БТ 30-5	14,9	27,0	11,1	1,942	4478	891	565	0,63
6.	БТ 60-5	14,9	26,9	11,0	1,726	4445	786	557	0,71
7.	БТ 90-5	15,0	26,9	11,0	1,706	4475	781	544	0,70
Вариант 2
8.	БТ 30-0	14,8	22,0	11,1	1,942	1002	384	549	1,43
9.	БТ 60-0	15,0	21,8	11,0	1,726	1020	348	420	1,21
10.	БТ 90-0	15,1	21,9	11,0	1,706	1034	349	418	1,20
11.	БТ 30-5	14,9	27,0	11,1	1,942	1016	390	565	1,45
12.	БТ 60-5	14,9	26,9	11,0	1,726	1007	344	557	1,62
13.	БТ 90-5	15,0	26,9	11,0	1,706	1020	344	544	1,58
Вариант 3
14.	БТ 30-0	14,8	-	11,1	1,942	2188	425	549	1,29
15.	БТ 60-0	15,0	-	11,0	1,726	2248	387	420	1,09
16.	БТ 90-0	15,1	-	11,0	1,706	2262	385	418	1,09
17.	БТ 30-5	14,9	-	11,1	1,942	2195	426	565	1,33
18.	БТ 60-5	14,9	-	11,0	1,726	2241	386	557	1,44
19.	БТ 90-5	15,0	-	11,0	1,706	2255	384	544	1,42

Анализ результатов сравнения (табл. 1) показывает, что средние значения отношения опытных и теоретических моментов образования трещин опытных образцов серии I составляют для:
· варианта 1 - 0,775 при максимальных и минимальных значениях 0,96 и 0,63 соответственно.
· варианта 2  - 1,415 при максимальных и минимальных значениях 1,62 и 1,2 соответственно;
· варианта 3 - 1,28 при максимальных и минимальных значениях 1,44 и 1,09 соответственно;
Проведенный анализ показал, что наилучшая сходимость результатов расчета с опытными данными наблюдается в третьем варианте. За основу принимаем 3-й вариант расчета элементов со сквозными отверстиями по трещиностойкости при кручении.
При исследовании сквозных балок на действие изгиба с кручением в основу была положена методика, разработанная в исследовании [6].
Предложенный в работе [6] расчетный аппарат по трещинообразованию железобетона был разработан на основе метода графиков взаимодействия.
В результате проведенных исследований для элементов прямоугольного сечения была определена предельная область по образованию трещин при совместном действии изгиба и кручения. Графически эта предельная область представлена на рис. 1.
Эта область описывается следующими выражениями:
1) при ψ  < 0,65 и  < 2/3,      ;       (4)
2) при 0,65 ≤ ψ≤0,95,             (5)
3) при ψ> 0,95 и ,            (6)
где  - соотношение между действующими моментами и моментами инерции сечения относительно главных осей.

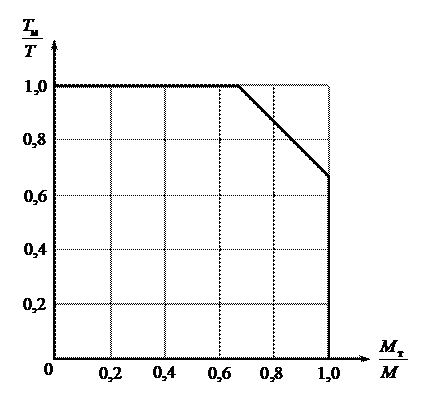
Рис. 1. График взаимодействия изгибающих и крутящих моментов при трещинообразовании

С целью определения взаимного влияния кручения и изгиба на процесс трещинообразования нами исследование проводилось в следующем порядке:
- по формуле (3) для всех образцов были определены теоретические значения моментов образования трещин Т_сrс;
- по формулам (126-139) СНиП [8] аналогичные расчеты были осуществлены в предположении действия только изгибающего момента М_сrс;
- были вычислены отношения опытных и теоретических моментов трещинообразования рассмотренных образцов.
Результаты проведенных расчетов приведены в табл. 2. Как видно из этой таблицы при интенсивном кручении с изгибом, как и ожидалось, изгиб не оказывает влияние и трещиностойкость и может определяться из расчета только на кручение, то есть по формуле (4).

Таблица № 2
Сравнение опытных и теоретических моментов трещинообразования

Проведенными исследованиями установлено, что:

1. Момент образования трещин при кручении балок со сквозными отверстиями опережал в среднем 8…10 % момент образования трещин балки-эталона сплошного сечения.
2. Плотность образования трещин в балках со сквозными отверстиями при изгибе с кручением существенно выше, чем при кручении.
3. Длина отверстия практически не оказывает заметного влияния на трещиностойкость элементов со сквозными отверстиями.
4. Предложенная формула (3) с достаточной для практических расчетов точностью позволяет оценить трещиностойкость железобетонных элементов со сквозными отверстиями при кручении.
5. Оценку трещиностойсти железобетонных элементов со сквозными отверстиями при интенсивном кручении с изгибом можно произвести формулой (4), которая ранее была получена для элементов прямоугольного сечения.

Литература:

1. Байрамуков  С.Х., Касаев  Д.Х. Оценка прочности железобетонных элементов, подвергнутых нескольким силовым факторам при статическом и динамическом воздействии [Текст]: Монография /  С.Х.  Байрамуков, Д.Х.   Касаев.  - Черкесск  ГОУ  ВПО КЧГТА, 2010 - 214 с.
2.Бескопыльный А.Н., Веремеенко А.А.  Методика экспериментального исследования предварительных напряжений в образце при вдавливании индентора [Электронный ресурс]  // «Инженерный вестник Дона», 2012.- №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1367 (доступ свободный) - Загл. с экрана. – Яз.рус.
3.Касаев Д.Х. Прочность элементов прямоугольного сечения при кручении [Текст] //Журнал// Бетон и железобетон. -1987. - №12 – С.23.
4.Касаев Д.Х. Прочность элементов таврового сечения при кручении [Текст]  // Совершенствование методов расчета железобетона. Ростов-на-Дону: РИСИ, 1988. –С.116-120.
5.Касаев Д.Х., Дудов М.Б., Дюрменова С. С. Прочность железобетонных балок с круглыми отверстиями при кручении [Текст] //Сборник материалов III международной научно-практической конференции «Проблемы строительства, инженерного обеспечения и экологии городов». – Пенза, 2001. – С. 9-11.
6.Касаев Д.Х. Прочность элементов железобетонных конструкций при кручении и изгибе с кручением [Текст]: Монография / Д.Х. Касаев.  -  Ростов н/Д.: Изд-во Рост. ун-та, 2001.-176с.
7.Косенко Е.Е., Косенко В.В., Черпаков А.В.  К вопросу о влиянии геометрических размеров на прочностные характеристики арматурных сталей  [Электронный ресурc] // «Инженерный вестник Дона», 2012.- №4. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4y2010/318 (доступ свободный) - Загл. с экрана. – Яз.рус.
8.СНиП 2.03.01-84* Бетонные и железобетонные конструкции. Нормы проектирования. - М.: Стройиздат. 1989. - 79 с.
9.Mansur  M. A., Paramasivam  P. Reinforced Concrete Beams with small Opening in Bending and Torsion //ACI Journal. 1984. - N. 81. - PP. 180-185.
10.Wafa F., Hasnat Abul, Akhtaruzzaman Ali A. Prestressed Concrete Beams with Opening under and Bending //Journal of Structural Engineering – ASCE. 1989. - N. 11. Vol. 115. PP. 2727-2739.