Динамическое управление информационными потоками в телекокоммуникационных сетях
Аннотация
Современная телекоммуникационная сеть (Т-сеть) – это объект высокой структурной сложности, полученный путем синтеза двух исходно независимых сетей – связи и вычислительных сетей. Т-сеть – система, работающая в случайной среде, а это приводит к необходимости решения задач, относящихся к теории массового обслуживания. К таким задачам относятся и вопросы управления информационными потоками в сети путем адаптации ее структуры к состоянию входных и выходных потоков. Теория построения Т-сетей находятся на стадии становления, поэтому рассматриваемая проблема, является актуальной. Ключевые слова: телекоммуникационная сеть, дисциплина обслуживания, динамическое управление, "дейзи-кольцо", порядковая логика
Таганрогский технологический институт
Южного федерального университета
Современная телекоммуникационная сеть (Т-сеть) – это объект высокой структурной сложности, полученный путем синтеза двух исходно независимых сетей – связи и вычислительных сетей. Т-сеть – система, работающая в случайной среде, а это приводит к необходимости решения задач, относящихся к теории массового обслуживания. К таким задачам относятся и вопросы управления информационными потоками в сети путем адаптации ее структуры к состоянию входных и выходных потоков (рис.1). Следует отметить, что теория построения Т-сетей находятся на стадии становления [1], поэтому рассматриваемая проблема, на наш взгляд, является актуальной.
Рис. 1. Обобщенная структура коммутационной подсистемы
Как видно из структуры, особое место в коммутационной подсистеме занимает система управления, которая осуществляет контроль за сбором, обработкой и в дальнейшем перемещением трафика в Т-сетях, распределением сетевых коммутационных ресурсов в соответствии с заданными приоритетами. Очевидно, что применение в составе коммутационной структуры систем динамического управления информационными потоками обеспечит необходимое качество функционирования сети, оперативную реакцию на малоинерционные ситуации в реальном масштабе времени. Динамическое управление распределением потоков может быть осуществлено как за счет управления структурой сети путем изменения емкости пучков каналов или перераспределением каналов сети при изменении информационных взаимодействий между отдельными парами узлов коммутации, так и за счет управления путями передачи потоков без изменения структуры сети [2]. Очевидно, что второй способ является как экономически, так и аппаратно более выгодным, поскольку изменения структуры сети минимальны.
Постановка задачи: на основе анализа традиционных методов управления обслуживанием информационных потоков, алгоритмов аппаратного и программного упорядочивания данных необходимо представить оптимальный по времени метод динамического управления потоками информации и осуществить синтез системы со следующими функциями: формирование управляющей информации для перестройки дисциплины обслуживания на основании параметров состояния входного потока (статического приоритета, величины штрафа за потерю заявки, скорости «старения» заявки в очереди на обслуживание); выбор оптимального алгоритма управления в реальном масштабе времени в зависимости от загрузки системы.
Статический приоритет p поступившей в систему заявки оценивают с учетом значений коэффициентов штрафа за задержку в обслуживании в единицу времени (или за потерю) и длительности ее обслуживания:
. (1)
Динамический приоритет определяется путем пересмотра очереди заявок в коммутационной подсистеме Т-сети с учетом времени пребывания каждой из них и функции изменения приоритета заявки во времени. Время пребывания j-й заявки может быть оценено выражением:
, (2)
где 
- время ожидания обслуживания (сумма времени пребывания заявки в очереди до начала обслуживания и времени ожидания в очереди в прерывном состоянии); 
- длительность обслуживания j-ой заявки, 
- номер заявки.
Если 
- предельно допустимое время пребывания j-ой заявки в подсистеме, то необходимо выполнить условие:
, (3)
которое соблюдается только за счет изменения времени ожидания обслуживания. Причем, при уменьшении длительности ожидания обслуживания приоритет заявки может повышаться, так как со временем вероятность превышение допустимого времени ожидания увеличивается. Очевидна идея по перестройке очереди с целью исключения потери «стареющих» заявок [3].
Если допустить, что 
- функция изменения приоритета j-ой заявки от времени 
, то приоритет j-ой заявки пропорционален 
- первой производной этой функции, 
- может быть расценен как интервал между соседними значениями времени, в которых пересматриваются приоритеты заявок, находящихся в очереди.
Приоритет находящихся в очереди заявок одного типа, для которых одинаковы отношения 
, целесообразно распределять пропорционально первым производным функций изменения приоритетов:
. (4)
С учетом неравенств (1) и (4) динамический приоритет заявок, находящихся в очереди к коммутационной схеме, распределяют в соответствии с
, (5)
то есть из двух заявок (j,k), находящихся на обслуживании к коммутационной схеме, высший приоритет присваивается той заявке, для которой больше значение 
. В зависимости от неравенства (5) заявка типа j имеет высший приоритет.
Таким образом, для управления очередью заявок в коммутационной подсистеме каждая (для примера j-ая) поступающая в систему заявка должна характеризоваться следующими параметрами: 
, где 
- машинное (технологическое) время поступления заявки в информационно-вычислительный телекоммуникационный комплекс. После вычисления приоритетов по зависимости неравенства (5) проверяют условие неравенства (3). При этом время ожидание заявки j-ого типа, которой присвоен в масштабе реального времени p-й приоритет, определяется как:
. (6)
Для i-ой заявки должно выполняться условие:
. (7)
При невыполнении неравенства (7) система снимает i-ю заявку (как исключительный случай) с обслуживания и в информационной модели объекта заменяет 
значением ее предыстории.
Обобщенная структурная схема системы динамического управления, реализующая дисциплину обслуживания очереди заявок с динамически изменяемыми приоритетами, представлена на рисунке 2 [3]:
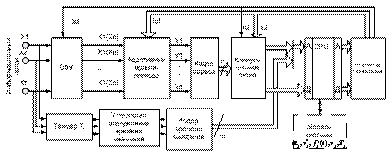
Рис. 2. Структурная схема адаптивной системы динамического управления очередями
В данной структуре матрицы 
и 
- набор в матричной форме сигналов, управляющих процессом коммутации заявок на входе информационно-вычислительного комплекса (CPU) и задающих наиболее приоритетный вход и порядок обслуживания соответственно, причем:
. (8)
Применение динамической дисциплины целесообразно при быстроменяющихся во времени параметрах входных информационных потоков, поскольку дисциплина обслуживания таких заявок по алгоритму с фиксированным приоритетом в соответствии с (1) приводит к увеличению вероятности их «старения» в системе, то есть к возможной потере.
Для реализации дисциплин обслуживания очереди заявок с динамически изменяемыми приоритетами необходимы системы управления, построенные на перепрограммируемом элементном базисе. В основу синтеза адаптивного мультиплексора системы динамического управления и устройства определения времени ожидания заявок в очереди положен математический аппарат порядковой логики [4], посредством которого был разработан новый класс кольцеподобных систем управления очередями по принципу «дейзи-кольцо» с динамически изменяемыми приоритетами в соответствии с информационной моделью входного потока.
Математическая модель системы динамического управления может быть описана с помощью элементов порядковой логики (логического определителя 
, квазиматрицы) [4]:
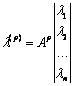, (9)
где 
- приоритет; 
- элементы квазиматрицы-столбца, соответствующие заявкам 
; 
- логический определитель (ЛО) квазиматрицы 
, который может быть задан в КНФ или ДНФ. При раскрытии ЛО:
(10)
получают соответственно упорядоченные ряды (очереди):
(11)
соответствии с назначенными приоритетами 
согласно оценкам (
- i-ая заявка с p-приоритетом)
Логическая модель системы динамического управления для n информационных заявок в результате порядково-логического синтеза может быть описана системой n логических уравнений,
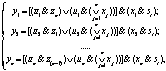, (12)
где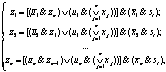 
при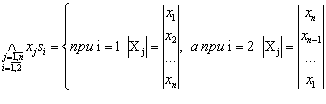
,
где 
- i-ый входной порт i-ой заявки; 
- выходной порт; 
- матрица управляющих сигналов, формирующих упорядоченный ряд, 
и задающих наиболее приоритетный вход; 
- матрица управляющих сигналов, задающих направление очереди 
или 
.
Для формирования матрицы управляющих сигналов 
, задающий наиболее приоритетный вход коммутационной схемы, предназначен кодер времени ожидания (КВО). При поступлении каждой заявки на вход системы динамического управления таймером фиксируется ее время прихода. Если заявка не обслуживается сразу после прихода, то после каждого такта генератора импульса определяется разность между текущим временем на таймере и временем прихода заявки. Данная разность поступает на КВО, в котором происходит сравнивание данной разности с априорным предельным временем ожидания.
Данное неупорядоченное множество значений длительностей ожидания 
, (коды времени представлены m-разрядным двоичным кодом), можно записать в виде квазиматрицы-столбца [3],
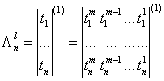(13)
где 
- j-й разрядный коэффициент 
.
Способ раскрытия логического определителя (13) для вычисления максимального элемента 
в ДНФ состоит в определении на первом этапе максимального разрядного коэффициента 
m-го разряда путем логического сложения элементов m-го столбца матрицы: 
. Теперь осуществим определение столбца адресно-разрядных коэффициентов m-го разряда:
, 
(14)
где 
- инверсное значение 
; 
- адресно-разрядный коэффициент m-го разряда i-й кодовой комбинации, 
.
Далее на каждом j-м этапе производиться рекурсивное вычисление соответственно разрядных коэффициентов 
и адресно-разрядных коэффициентов 
от старших разрядов к младшим согласно следующим правилам:
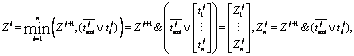
На m-м последнем этапе получают экстремальное значение разности текущего времени и времени поступления заявки, представленной в m-разрядном двоичном коде, 
и столбец адресно-разрядных коэффициентов первого разряда:
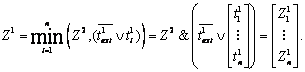(15)
Столбец (15) может содержать один или несколько единичных элементов, соответствующих заявкам с максимальной разностью. При наличии одного единичного элемента применение к формуле (15) функции кодирования позволяет получить адрес такого канала. Наличие нескольких единичных элементов свидетельствует о том, что имеется несколько каналов с одинаковым временем ожидания обслуживания, в данном случае необходим выбор того канала, которому присвоен больший заранее заданный приоритет, например, по возрастанию порядкового номера заявки.
В общем случае операция кодирования имеет вид: 
где 
- операция формирования адреса i-го параметра с учетом заранее заданного приоритета по обслуживанию заявок в очереди, позволяя получить адрес параметра с экстремальным значением времени ожидания.
Выводы:
- разработан алгоритм динамического управления информационными потоками в Т-сетях на основании интегрального критерия
;
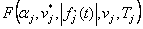- такой алгоритм предназначен для обслуживания быстроменяющихся во времени информационных потоков, что актуально для мультисервисных Т-сетей;
- предложен метод синтеза адаптивной системы управления информационными потоками, позволяющий при минимальных аппаратных затратах формировать
рядов очередей, где n – число информационных входов.
Список литературы
1. Ершов В.А., Кузнецов Н.А. Мультисервисные телекоммуникационные сети. – М: Изд-во МГТУ им. Н.Э.Баумана, 2003, 432 с.
2. Лазарев В.Г., Лазарев Ю.В. Динамическое управление потоками информации в сетях связи. – М.: Радио и связь. 1983. – 216 с.
3. Колыхан Н.В., Самойленко А.П. Синтез адаптивной системы прерывания телекоммуникационных комплексов// Известия ТРТУ. Материалы LII научно-технической конференции профессорско-преподавательского состава ТРТУ. Таганрог: Изд-во ТРТУ, 2006 №9(06), с.15-20
4. Левин В.И. Структурно-логические методы исследования сложных систем с применением ЭВМ – М: Наука – 1987. – 304 с.
20 июня 2008 г.