Определение влияния ветровых нагрузок на антенное сооружение
Аннотация
В данной работе ставится задача оценки аэродинамических воздействий на антенное сооружение с учетом формы антенны, скорости ее вращения и стохастических характеристик скоростного напора ветрового потока.
Рассматривается объект воздействия ветровых нагрузок - антенна, закрепленная на вертикальной штанге, с возможностью вращения вокруг нее в азимутальной плоскости и поворотом на ограниченный угол в угломестной плоскости. Ключевые слова: антена, влияние, ветровая нагрузка, передающая функция, аэродинамические свойства05.13.18 - Математическое моделирование, численные методы и комплексы программ
Определение влияния ветровых нагрузок на антенное сооружение
П.И. Николас
Технические объекты, предназначенные для эксплуатации на открытом воздухе, обычно рассчитывают на ветровые нагрузки, которые определяются в соответствии со строительными нормами. В радиотехнике достаточно часто встречается задача расчета на ветровые нагрузки антенных устройств, которые эти правила не охватывают. Особенностью антенных систем является то, что они вращаются с достаточно высокой угловой скоростью и имеют нерегулярную форму, а, следовательно, на практике наблюдаются существенные изменения значений аэродинамического коэффициента за период одного оборота антенны. Поэтому для антенн обычно используются натурные методы испытаний и продувки в аэродинамических трубах, которые требуют больших ресурсных затрат и не отражают особенностей динамического взаимодействия вращающегося объекта и ветрового потока.
В данной работе ставится задача оценки аэродинамических воздействий на антенное сооружение с учетом формы антенны, скорости ее вращения и стохастических характеристик скоростного напора ветрового потока.
Рассматривается объект воздействия ветровых нагрузок - антенна, закрепленная на вертикальной штанге, с возможностью вращения вокруг нее в азимутальной плоскости и поворотом на ограниченный угол в угломестной плоскости (рис.1).
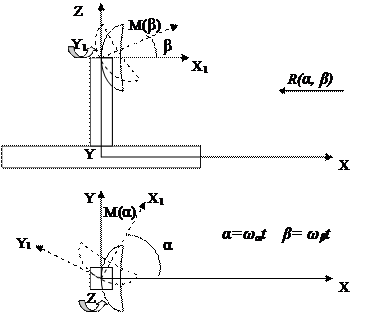
Рисунок 1. Схема воздействия ветрового потока R(α,β)
С неподвижным основанием связана декартова система координат X, Y, Z, а с зеркалом антенной системы - X1, Y1, Z1. Ветровой поток направлен вдоль оси X. Угол поворота вокруг оси Z1 (α) определяет положение антенны по отношению к вектору скорости ветрового потока в азимутальной плоскости, угол поворота вокруг оси Y1 (β) - в угломестной.
Нагрузка на антенную систему при неподвижной конструкции определяется выражениями:
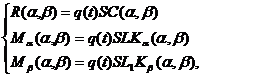 (1)
(1)
где R(α,β) – аэродинамическая сила, приложенная к АС;
Мα, Mβ – аэродинамические крутящие моменты относительно азимутальной и угломестной осей АС;![]() – скоростной напор ветрового потока;
– скоростной напор ветрового потока;
С(α, β), K(α,β) – аэродинамические коэффициенты силы и момента;
S, L, L1 – площадь и линейные размеры раскрыва отражателя.
Аэродинамические коэффициенты силы и моментов определяются экспериментально. В частных случаях (для отражателей простой формы) они могут быть рассчитаны. Скоростной напор q(t) является случайной стационарной функцией времени, описываемой выражением [1]:
![]() ,
,
где ![]() – среднее значение скорости ветра;
– среднее значение скорости ветра;![]() – пульсации скоростного напора.
– пульсации скоростного напора.
Корреляционная функция пульсаций скоростного напора Kq(τ) имеет вид:
![]()
где a, b – известные коэффициенты, определяемые экспериментально.
Нормированная спектральная плотность G(ω) функции q(t), определяемая как преобразование Фурье от функции Kq(τ), имеет вид:
![]() m2 = a2 +b2; k = a2 - b2;
m2 = a2 +b2; k = a2 - b2;
С учетом условий эксплуатации, при которых следящая системы осуществляет независимое управление движением АС вокруг азимутальной и угломестной осей, необходимость корректировки угломестного положения сравнительно редка (β = const), а в установившемся режиме вращение конструкции по азимуту происходит с постоянной угловой скоростью (α = ωαt), система уравнений (1) может быть упрощена:
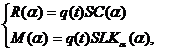 (2)
(2)
а функция С(α) = С(ωαt) становится периодической функцией времени и может быть разложена в ряд Фурье:
![]()
где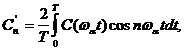
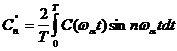 .
.
Аналогичные преобразования необходимы для функции Kα(α). Тогда система уравнений (2) может быть представлена в виде:
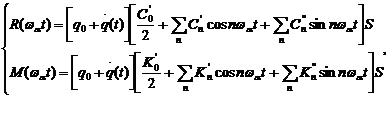
или
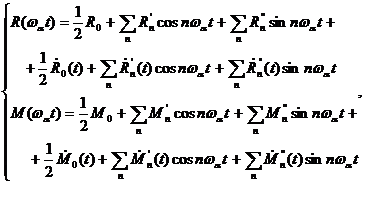 (3)
(3)
где 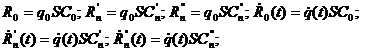
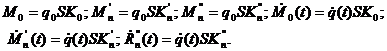
Таким образом, полная аэродинамическая сила и крутящий момент относительно азимута, действующие на вращающуюся АС, могут быть представлены в виде гармонических рядов, содержащих детерминированные и случайные части - слагаемые, включающие в себя пульсацию скоростного напора, являющуюся случайной функцией времени, статистические характеристики которой известны.
Каждое такое слагаемое может быть представлено как произведение случайной и детерминированной функций времени:
![]()
и ее корреляционная функция имеет вид [2]
![]() .
.
Функцию KF(τ) можно представить в виде суммы
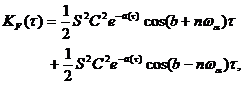 (4)
(4)
и с ее помощью определить статистические характеристики случайных слагаемых полной аэродинамической силы и крутящего момента.
Действие полной аэродинамической силы R(ωαt) и момента M(ωαt) из системы уравнений (3) на вращающиеся части АС необходимо учитывать при моделировании следящей системы, причем при наличии в ней последовательного цифрового корректирующего звена, выполненного в виде микроконтроллера, учет изменяющегося внешнего воздействия можно использовать при расчете управляющего воздействия [3].
В уравнение динамики следящей системы входит величина момента нагрузки, приведенного к валу двигателя, в котором необходим учет ветровой нагрузки:
![]() (5)
(5)
где ![]()
μ – коэффициент трения, d – внутренний диаметр подшипника.
Уравнение (5) можно записать в виде:
![]() ,
,
при этом расчет Mветр необходимо вести с помощью корреляционной функции вида (4).
Из полученных формул для расчета ветровых нагрузок видно, что для вращающихся частей АС аэродинамический коэффициент есть периодическая функция времени, для неподвижных частей конструкции он определяется конечным числом, зависящим от направления ветровой нагрузки. Спектр нагрузки на вращающиеся элементы конструкции АС за счет появления дополнительных гармонических множителей расширяется и зависит от угловой скорости вращения.
Таким образом, в статье предложен способ определения влияния ветровых нагрузок на антенное сооружение. Использование описанной методики определения аэродинамических воздействий на антенну возможно как на этапе моделирования, так и при разработке АС. Это позволяет сократить, а в некоторых случаях избежать проведения натурных испытаний, а также получить устойчивые статические и динамические характеристики системы.
Литература
1. Николаенко Н.А. Вероятностные методы динамического расчета машиностроительных конструкций. М., «Машиностроение», 1967.
2. Венцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М., «Наука», 1991.
3. Ерофеев А.А. Теория автоматического управления: Учебник для вузов. – СПб.: Политехника, 2005.
20 июня 2008 г.