Конечноэлементный анализ применимости прикладных теорий расчета пьезоэлектрического устройства накопления энергии стековой конфигурации
Аннотация
Дата поступления статьи: 18.03.2014В работе рассматривается основной элемент устройства накопления энергии представляющий собой пьезоэлектрический генератор (ПЭГ) цилиндрической формы с прикрепленной к нему инерционной массой. Осуществлено конечноэлементное моделирование работы устройства при активной нагрузке во внешней электрической цепи. Основная цель работы провести сравнение выходного потенциала и частотных характеристик такого устройства с известными в литературе моделями систем со сосредоточенными параметрами. На основе этих моделей можно получить аналитические зависимости параметров ПЭГ с его геометрическими характеристиками и механическими свойствами используемых материалов. Однако вопрос об области применимости этих формул остается открытым. В работе на основе численного анализа конечноэлементных моделей ПЭГ в пакете ANSYS получено сравнение с аналитическими формулами, указаны значения некоторых параметров упрощенных моделей и установлены границы их применимости.
Ключевые слова: накопление энергии, ПЭГ, пьезокерамика, эффективная масса, резонансная частота, МКЭ.
Введение
Пьезоэлектрические устройства накопления энергии являются альтернативным источником энергии, которые позволяют собирать энергию от маломощных источников в окружающей среде, например, вибрация от качающихся мостов, движущихся механизмов и т.д. Устройства накопления энергии, в частности, пьезоэлектрические широко изучаются в различных областях техники от аэрокосмической области до бытовых устройств и этим обусловлен интерес их исследования [1 - 11].
В последнее время были изучены различные подходы к моделированию пьезоэлектрических устройств накопления энергии. Большинство моделей были созданы на основе системы с одной степенью свободы – «пружина с инерционной массой». Работы [1 - 5] посвящены построению моделей ПЭГ на основе колебаний механической системы с сосредоточенными параметрами. Использование таких систем является удобным модельным подходом, так как позволяет получить аналитические зависимости между выходными параметрами ПЭГ (потенциалом, мощностью и т.п.) и электрическими, механическими характеристиками и сопротивлением внешней электрической цепи. Задача формулируется в виде системы обыкновенных дифференциальных уравнений состоящих из уравнения движения с учетом пьезоэлектрического эффекта [2 - 4]. В работе [5] на основе этих моделей проведен учет случайных колебаний ПЭГ. В работе [6] использован метод Релея-Ритца на основе разложения по собственным формам колебаний. В работе [7] построено решение в аналитической форме для одномерной модели устройства. В работе [8] разработана модифицированная модель [6] для определения оптимальных параметров ПЭГ. В работе [9] исследование тонкой биморфной пьезопластины проводится в рамках приближенной теории на основе уравнений Тимошенко. В работе [10] исследуется вопрос оптимизации конструкции изгибного ПЭГ в зависимости от условий крепления. Одним из средств улучшения характеристик ПЭГ является использование пьезокомпозиционных материалов, так в работе [11] представлены результаты вычислительных экспериментов по определению характеристик пористой пьезокерамики по методологии, включающей метод эффективных модулей.
В настоящей работе изучаются области применимости этих упрощенных моделей на основе строгих трехмерных математических постановок для упругих и электроупругих сред и анализа их конечноэлементных аналогов в пакете ANSYS.
1. Приближенная и точная постановка задачи
В работе рассматривается ПЭГ являющийся главным элементом устройства накопления энергии, имеющий стековую конструкцию, где активный элемент состоит из одного (рис. 1а, 1б) или нескольких слоев пьезокерамики (рис. 1в), поляризованных по толщине в форме короткого цилиндра и переходных упругих слоев такого же радиуса. Верхняя и нижняя торцевые поверхности пьезодиска полностью электродированы. Весь пакет заключен в цилиндрический корпус, жестко закрепленный по нижнему основанию. Рассматриваемое устройство включается в электрическую цепь с активным сопротивлением ![]() (рис. 1а).
(рис. 1а).
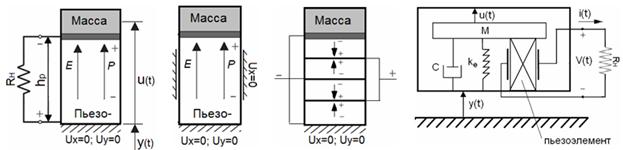 а) б) в) г)
а) б) в) г)Рис. 1. Модель ПЭГ стековой конфигурации. а) свободная боковая поверхность (первая модель); б) условия гладкого контакта (вторая модель); в) модель с несколькими слоями пьезокерамики; г) эквивалентная модель с сосредоточенными параметрами.
Рассматривается ПЭГ для двух моделей с различными механическими условиями на боковой поверхности. В первой модели (рис. 1а) только нижняя поверхность пьезоэлемента закреплена в подвижной системе и совершает вертикальные колебания вместе с ней, во второй цилиндрическая поверхность пьезоэлемента закреплена по радиальному направлению – условия гладкого контакта (рис. 1б).
При этом задается ![]() - вертикальное перемещение нижней поверхности ПЭГ:
- вертикальное перемещение нижней поверхности ПЭГ:
![]() (1)
(1)
где ![]() – амплитудное колебание (
– амплитудное колебание (![]() мм),
мм), ![]() – частота вынужденных колебаний в Гц.
– частота вынужденных колебаний в Гц.
В конструкции использовались следующие материалы: пьезоэлемент – пьезокерамика PZT-5H; инерционный элемент – сталь. Значения электроупругих модулей керамики PZT-5H приведены в таблице 1.
Таблица № 1
Материальные константы пьезокерамики PZT-5H:
(ГПа) |
|
|
|
|
|
|
|
|
|
|
126 |
55 |
53 |
117 |
35.3 |
-6.5 |
23.3 |
17 |
1710 |
1470 |
![]() Φ/м; плотность
Φ/м; плотность ![]() кг/м3;
кг/м3; ![]() - коэффициент демпфирования.
- коэффициент демпфирования.
Упругие свойства изотропных материалов задаются с помощью модуля Юнга Е и коэффициента Пуассона ν. Характеристики конструкционных материалов – сталь: плотность![]() кг/м3; модуль Юнга
кг/м3; модуль Юнга ![]() Па; коэффициент Пуассона
Па; коэффициент Пуассона ![]() .
.
Эквивалентная механическая модель. Для ПЭГ стековой конфигурации, работающего на частоте близкой к собственной, эквивалентная модель с одной степенью свободы (рис. 1г) может быть построена на основе сочетания уравнений актуатора и датчика, полученного для электромеханически-связанных систем [1]:
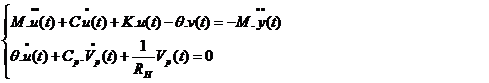 (2)
(2)
Из уравнений (2) можно определить значение выходного потенциала ![]() по формуле [1]:
по формуле [1]:
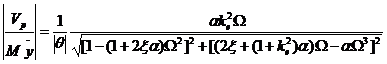 (3)
(3)
ПЭГ характеризуется двумя собственными частотами: резонансная частота ![]() соответствует коэффициенту демпфирования
соответствует коэффициенту демпфирования ![]() , сопротивлению активной нагрузки
, сопротивлению активной нагрузки ![]() (короткое замыкание) и антирезонансная частота
(короткое замыкание) и антирезонансная частота ![]() -
- ![]() ,
, ![]() (разомкнутой цепи). Значения fn и
(разомкнутой цепи). Значения fn и ![]() можно выразить в виде [1]:
можно выразить в виде [1]:
![]() и
и ![]() , (4)
, (4)
![]()
![]() ,
, ![]() ;
; 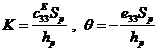 (5)
(5)
где ![]() – напряжение;
– напряжение; ![]() - коэффициент эффективного демпфирования;
- коэффициент эффективного демпфирования; ![]() - эффективная емкость.
- эффективная емкость. ![]() - отношение частота;
- отношение частота; ![]() – безразмерные постоянные времени;
– безразмерные постоянные времени; ![]() – жесткость пьезоэлектрического слоя, когда система находится в состоянии короткого замыкания;
– жесткость пьезоэлектрического слоя, когда система находится в состоянии короткого замыкания; ![]() - силовой коэффициент;
- силовой коэффициент; ![]() - эффективная жесткость;
- эффективная жесткость; ![]() - площадь поверхности пьезоэлемента;
- площадь поверхности пьезоэлемента; ![]() - высоты пьезоэлемента; и
- высоты пьезоэлемента; и ![]() – эффективная масса, можно записать в виде [1]
– эффективная масса, можно записать в виде [1]
![]() , (6)
, (6)
![]() – масса инерционная;
– масса инерционная; ![]() – масса пьезоэлемента;
– масса пьезоэлемента; ![]() – коэффициент приближенной эффективной массы (в [1] принято, что коэффициент n = 3).
– коэффициент приближенной эффективной массы (в [1] принято, что коэффициент n = 3).
Основной целью работы является исследования области применимости одномерной модели (2) - (6) с помощью ее сравнения с конечноэлементным расчетом в программных пакетах ACELAN и ANSYS.
Континуальные постановки задач электроупругости. Стековое пьезоэлектрическое устройство накопления энергии (рис. 1а, 1б) представляет собой составное упругое и электроупругое тело, которое совершает малые колебания в подвижной системе координат. Прямолинейное вертикальное движение этой системы (рис. 1) задается законом ![]() , в соответствии с которыми движется основание устройства. В этих условия достаточно адекватной математической моделью функционирования устройства является начально-краевая задача линейной теории электроупругости [12].
, в соответствии с которыми движется основание устройства. В этих условия достаточно адекватной математической моделью функционирования устройства является начально-краевая задача линейной теории электроупругости [12].
Рассмотрим некоторый пьезопреобразователь ![]() , представленный набором областей
, представленный набором областей ![]() ;
; ![]() ;
; ![]() со свойствами пьезоэлектрических материалов и набором областей
со свойствами пьезоэлектрических материалов и набором областей ![]() ;
;![]() ;
; ![]() со свойствами упругих материалов. Будем считать, что физико-механические процессы, происходящие в средах
со свойствами упругих материалов. Будем считать, что физико-механические процессы, происходящие в средах ![]() и
и ![]() , можно адекватно описать в рамках теорий пьезоэлектричества (электроупругости) и упругости.
, можно адекватно описать в рамках теорий пьезоэлектричества (электроупругости) и упругости.
Для пьезоэлектрических сред ![]() предположим, что выполняются следующие полевые уравнения и определяющие соотношения:
предположим, что выполняются следующие полевые уравнения и определяющие соотношения:
![]() ;
; ![]() , (7)
, (7)
![]() ;
; ![]() , (8)
, (8)
![]() ;
; ![]() , (9)
, (9)
где ![]() – плотность материала;
– плотность материала; ![]() – вектор-функция перемещений;
– вектор-функция перемещений; ![]() – тензор механических напряжений;
– тензор механических напряжений; ![]() – вектор плотности массовых сил;
– вектор плотности массовых сил; ![]() – трехмерный вектор индукции электрического поля;
– трехмерный вектор индукции электрического поля; ![]() – тензор четвертого ранга упругих модулей, измеренных при постоянном электрическом поле;
– тензор четвертого ранга упругих модулей, измеренных при постоянном электрическом поле; ![]() – тензор пьезомодулей третьего ранга;
– тензор пьезомодулей третьего ранга; ![]() – тензор деформаций;
– тензор деформаций; ![]() – трехмерный вектор напряженности электрического поля;
– трехмерный вектор напряженности электрического поля; ![]() – функция электрического потенциала;
– функция электрического потенциала; ![]() – тензор второго ранга диэлектрических проницаемостей, измеренных при постоянной деформации;
– тензор второго ранга диэлектрических проницаемостей, измеренных при постоянной деформации; ![]() – неотрицательные коэффициенты демпфирования [12], а остальные обозначения стандартны для теории электроупругости, за исключением дополнительного индекса ”j”, указывающего на принадлежность к среде
– неотрицательные коэффициенты демпфирования [12], а остальные обозначения стандартны для теории электроупругости, за исключением дополнительного индекса ”j”, указывающего на принадлежность к среде ![]() с номером j.
с номером j.
Для сред ![]() с чисто упругими свойствами будем учитывать только механические поля, для которых примем аналогичные (7) - (9) полевые уравнения и определяющие соотношения в пренебрежении электрическими полями и эффектами пьезоэлектрической связности.
с чисто упругими свойствами будем учитывать только механические поля, для которых примем аналогичные (7) - (9) полевые уравнения и определяющие соотношения в пренебрежении электрическими полями и эффектами пьезоэлектрической связности.
К уравнениям (7) - (9) добавляются механические и электрические граничные условия, а также начальные условия в случае нестационарной задачи, среди которых отметим условие на электроде ![]() связанным с электрической цепью устройства накопления энергии.
связанным с электрической цепью устройства накопления энергии.
![]()
![]() , (10)
, (10)
где I - ток в цепи, который в случае свободного электрода равен нулю. В работе рассматриваются случаи подключения к электрической цепи с активным сопротивлением.
2. Численные расчеты
Как оказалось значение коэффициента приближенной эффективной массы n зависит от геометрических параметров конструкции и граничных условий. В настоящей работе изучено влияние значения высоты пьезоэлемента ![]() , массы инерционной
, массы инерционной ![]() и площади поверхности пьезоэлемента
и площади поверхности пьезоэлемента ![]() на этот коэффициент для двух моделей в случае свободного электрода.
на этот коэффициент для двух моделей в случае свободного электрода.
В начале рассматривается влияние высоты пьезоэлемента ![]() ,инерционной массы
,инерционной массы ![]() , и площади поверхности электрода
, и площади поверхности электрода ![]() на первую резонансную частоту
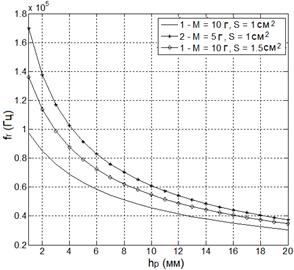
на первую резонансную частоту ![]() для двух модель (расчеты проводились в ANSYS). Полученные зависимости резонансных частот от высоты пьезоэлемента
для двух модель (расчеты проводились в ANSYS). Полученные зависимости резонансных частот от высоты пьезоэлемента ![]() , изменяющейся в интервале1 ÷ 20 мм приведены на рис. 2.
, изменяющейся в интервале1 ÷ 20 мм приведены на рис. 2.
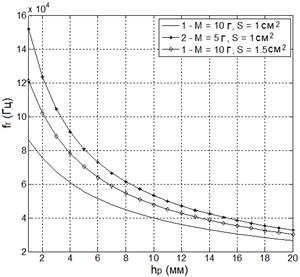 |
|
|
а) |
б) |
Рис. 2. а) - первая модель; б) - вторая модель.
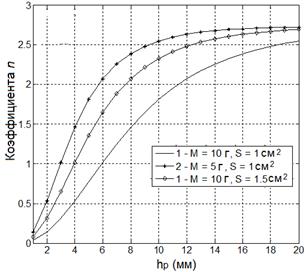
Далее рассматривается зависимость значения коэффициента n, входящего в формулу (6), от значения высоты пьезоэлемента ![]() , инерционной массы
, инерционной массы ![]() и площади поверхности электрода
и площади поверхности электрода ![]() .
.
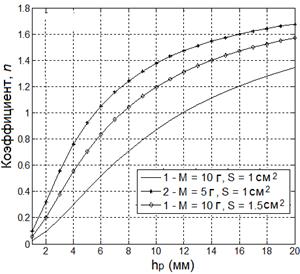
Значение коэффициента n находится из условия совпадения частот резонанса, вычисленных по соотношениям (4) и, рассчитанных с помощью конечноэлементной модели в пакете ANSYS (рис. 2). Полученные зависимости значения коэффициента приближенной эффективной массы n от высоты пьезоэлемента ![]() , инерционной массы
, инерционной массы ![]() , и площади поверхности электрода
, и площади поверхности электрода ![]() для двух моделей представлены на рис. 3.
для двух моделей представлены на рис. 3.
 |
|
|
а) |
б) |
Рис. 3. а) - первая модель; б) - вторая модель.
Из рис. 3 видно, что для обеих моделей значение коэффициента n возрастает с ростом высоты пьезоэлемента ![]() , и площади поверхности электрода
, и площади поверхности электрода ![]() , но убывает с ростом инерционной массы
, но убывает с ростом инерционной массы ![]() . Значение коэффициента n для первой модели меньше, чем для второй модели.
. Значение коэффициента n для первой модели меньше, чем для второй модели.
В итоге можно заключить, что значение коэффициента n не равно фиксированному значению 3 (как заявили авторы в [1]). Значение коэффициента n изменяется и зависит от геометрических параметров конструкции. Для второй модели, при значении ![]() cм2 (это значение был использовано в статье [1]), значение коэффициента n возрастает с ростом высоты пьезоэлемента
cм2 (это значение был использовано в статье [1]), значение коэффициента n возрастает с ростом высоты пьезоэлемента ![]() , и принимает значение2,7218 (≈ 3) при высоте
, и принимает значение2,7218 (≈ 3) при высоте ![]() мм. Таким образом, при использовании метода моделирования на основе систем с сосредоточенными параметрами нужно иметь в виду, что значение коэффициента n зависит от параметров устройства. Результаты, представленные на рис. 3 позволяют в зависимости от высоты пьезоэлемента
мм. Таким образом, при использовании метода моделирования на основе систем с сосредоточенными параметрами нужно иметь в виду, что значение коэффициента n зависит от параметров устройства. Результаты, представленные на рис. 3 позволяют в зависимости от высоты пьезоэлемента ![]() , инерционной массы
, инерционной массы ![]() , и площади
, и площади ![]() выбрать значение коэффициента n.
выбрать значение коэффициента n.
3. Сравнение выходного потенциала
В работе рассматривается выходное напряжение ПЭГ для второй модели в зависимости от частот вынужденных колебаний, изменяющихся в интервале 10 ÷ 80 кГц.
В начале сравнится выходное напряжение ![]() , вычисленное по соотношениям (3) и
, вычисленное по соотношениям (3) и ![]() , рассчитанное с помощью конечноэлементной модели, т.е. изучается влияние геометрических параметров устройства на значения коэффициентов n и
, рассчитанное с помощью конечноэлементной модели, т.е. изучается влияние геометрических параметров устройства на значения коэффициентов n и ![]() . Полученные результаты показывают, что значения коэффициента n и
. Полученные результаты показывают, что значения коэффициента n и ![]() изменяются в зависимости от геометрических параметров устройства и величины активного сопротивления
изменяются в зависимости от геометрических параметров устройства и величины активного сопротивления ![]() .
.
Так, при значении инерционной массы ![]() г, площади поверхности электроде
г, площади поверхности электроде ![]() cм2, полученные значения коэффициента n и
cм2, полученные значения коэффициента n и ![]() в зависимости от значений высоты пьезоэлемент
в зависимости от значений высоты пьезоэлемент ![]() , и активной сопротивления
, и активной сопротивления ![]() представлены в таб. 2.
представлены в таб. 2.
Таблица № 2
Значения коэффициента n и λ
|
|
RН |
0,1 кОм |
1 кОм |
10 кОм |
0,1 МОм |
1 МОм |
|
hp = 10 мм |
n |
1,81 |
1,81 |
1,81 |
1,61 |
1,61 |
|
λ |
1 |
1 |
1 |
1,02 |
1,02 |
|
|
hp = 20 мм |
n |
2,73 |
2,73 |
2,73 |
2,68 |
2,68 |
|
λ |
1,12 |
1,12 |
1,12 |
1,18 |
1,18 |
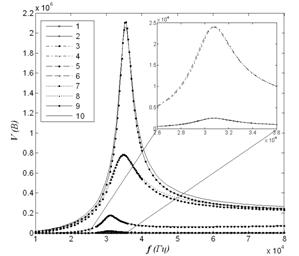
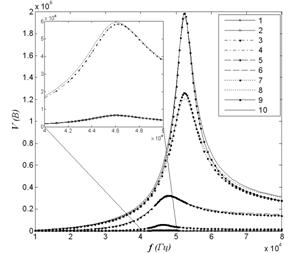
Результаты, представленные в таб. 2, показывают, что значение коэффициента n равно значению, рассчитанному выше (рис. 3) при не большом активном сопротивлении ![]() . При этом полученные зависимости выходного потенциала от частот вынужденных колебаний представлены на рис. 4а и 4б для значения высоты пьезоэлемента
. При этом полученные зависимости выходного потенциала от частот вынужденных колебаний представлены на рис. 4а и 4б для значения высоты пьезоэлемента ![]() мм и
мм и ![]() мм соответственно. Значения коэффициентов n и
мм соответственно. Значения коэффициентов n и ![]() соответствуют таб. 2. При этом кривые 1, 2 соответствуют
соответствуют таб. 2. При этом кривые 1, 2 соответствуют ![]() Ом; кривые 3, 4 –
Ом; кривые 3, 4 – ![]() кОм; кривые 5, 6 –
кОм; кривые 5, 6 – ![]() кОм; кривые 7, 8 –
кОм; кривые 7, 8 – ![]() МОм; кривые 9, 10 –
МОм; кривые 9, 10 – ![]() МОм;
МОм;
 |
|
|
а) - |
б) - |
Рис. 4. Кривые 1,3,5,7,9 соответствуют расчетам по формулам (3); кривые 2,4,6,8,10 - расчетам в ANSYS.
Сравнение результатов расчетов при установленных параметрах модели (коэффициенты n и ![]() ) показывает достаточно хорошее их совпадение, особенно в области частот, близких к резонансной частоте.
) показывает достаточно хорошее их совпадение, особенно в области частот, близких к резонансной частоте.
Далее рассматривается выходное напряжение ![]() в случаях, когда пьезоэлемент состоит из одного или двух, и четырех слоев пьезокерамики (рис. 1в). В том случае, когда устройство включено в электрическую цепь с активным сопротивлением
в случаях, когда пьезоэлемент состоит из одного или двух, и четырех слоев пьезокерамики (рис. 1в). В том случае, когда устройство включено в электрическую цепь с активным сопротивлением ![]() кОм. Значения
кОм. Значения ![]() мм,
мм, ![]() г и
г и ![]() cм2. Полученные зависимости выходного потенциала от частот вынужденных колебаний представлены на рис. 5.
cм2. Полученные зависимости выходного потенциала от частот вынужденных колебаний представлены на рис. 5.
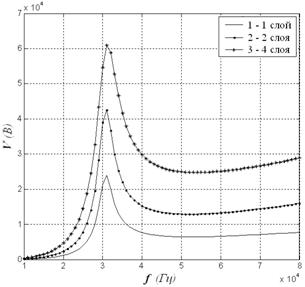
Рис. 5. – Зависимость электрического потенциала от вибрационной частоты.
Из рис. 5 видно, что значение электрического потенциала возрастает с ростом числа пьезоэлектрических слоев.
Выводы
Из приведенных выше результатов можно сделать следующий вывод, что при использовании метода моделирования систем с сосредоточенными параметрами, настройка каждой модели зависит от геометрических характеристик и конструкций модели. Метод исследования, который построен на модели с сосредоточенными параметрами дает первоначальное понимание проблемы, это приближение ограничивается одиночным режимом вибраций и в нем отсутствуют некоторые важные аспекты, связанные с формами колебаний и точным распределение деформаций, которые оказывают влияние на электрический отклик. В работе изучены области применимости модели на основе сосредоточенных параметров с одной механической степенью свободы с помощью ее сравнения с конечно-элементным расчетом в пакетах ACELAN и ANSYS. Исследование показало влияние структурных параметров на электрический отклик и необходимость учета этого обстоятельства при использовании упрощенных моделей. Проведенные расчеты результаты, которых представлены в виде графиков и таблиц позволяют выбрать рациональные коэффициенты приближенной эффективной массыn, для их использования в одномерных моделях.
Литература:
- DuToit N.E., Wardle B.L. Experimental verification of models for microfabricated piezoelectric vibration energy harvesters [Text] // AIAA J, 2007. – Vol.45. – pp.1126-1137.
- Roundy S., Wright P.K. A piezoelectric vibration based generator for wireless electronics [Text] // Smart Materials and Structures, 2004. – Vol.13. – pp.1131-1144.
- DuToit N.E., Wardle B.L., Kim S. Design considerations for MEMS-scale piezoelectric mechanical vibration energy harvesters [Text] // Journal of Integrated Ferroelectrics, 2005. Vol.71. – pp.121-160.
- Standards Committee of the IEEE Ultrasonics, Ferroelectrics, and Frequency Control Society “IEEE Standard on Piezoelectricity”, IEEE, New York, 1987. – pp.1-66.
- Adhikari S., Friswell M.I., Inman D.J. Piezoelectric energy harvesting from broadband random vibrations [Text] // Smart Materials and Structures, 2009. – Vol.18. – 115005 (pp.1-7).
- Sodano H.A., Park G., Inman D.J. Estimation of Electric Charge Output for Piezoelectric Energy Harvesting [Text] // Journal of Strain, 2004. – Vol.40. – pp.49-58.
- Erturk A., Inman D.J. Analytical Modeling of Cantilevered Piezoelectric Energy Harvesters for Transverse and Longitudinal Base Motions // In: Proceeding of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, IL, 7 -10 April 2008, Schaumburg, IL.
- Liao Y., Sodano A.H. Model of a Single Mode Energy Harvester and Properties for Optimal Power Generation [Text] // Smart Materials and Structures, 2008. – Vol.17. – 065026 (14pp), ISSN 0964-1726
- Шляхин Д. А. Вынужденные осесимметричные колебания тонкой круглой биморфной пластины ступенчато переменной толщины и жесткости [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://ivdon.ru/magazine/archive/n1y2013/1516 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Мартыненко А.В. Исследование параметров осесимметричного изгибного пьезоэлектрического преобразователя при различных граничных условиях [Электронный ресурс] // «Инженерный вестник Дона», 2010, №3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2010/206 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Наседкин А.В., Шевцова М.С. Сравнительный анализ результатов моделирования пористой пьезокерамики методами эффективных модулей и конечных элементов с экспериментальными данными [Электронный ресурс] // «Инженерный вестник Дона», 2013, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1615 (доступ свободный) – Загл. с экрана. – Яз. рус.
- Белоконь А.В., Наседкин А.В., Соловьев А.Н. Новые схемы конечно-элементного динамического анализа пьезоэлектрических устройств [Текст] // Прикладная математика и механика, 2002. – №.3. – С.491-501.