Расчетная модель с учетом зависимости вязкости и проницаемости пористого слоя от давления трехслойной гидродинамической смазки радиального подшипника, обладающего повышенной несущей способностью и демпфирующими свойствами
Аннотация
Дата поступления статьи: 09.04.2014В работе на основе уравнений Навье-Стокса, уравнения неразрывности с учетом зависимости вязкости от давления, уравнения Дарси с учетом зависимости проницаемости пористого слоя от давления дается метод формирования точного автомодельного решения задачи гидродинамического расчета радиального подшипника, работающего на трехслойном смазочном материале. В результате найдено поле скоростей и давлений в смазочных слоях и получены аналитические выражения для компонент вектора поддерживающей силы и силы трения. Найдены рациональные по несущей способности значения параметров характеризующих различные аспекты функционирования рассматриваемого узла трения, а именно: профиль опорной поверхности; особенные взаимодействия смазочной жидкости с поверхностями узла трения с учетом зависимости вязкости от давления (образование промежуточных слоев смазки с разными вязкостями).
Ключевые слова: трехслойная смазка, поддерживающая сила, адаптированный профиль, стратифицированное течение.
Анализ существующих работ [1 – 11], посвященных расчету подшипников скольжения, показывает, что приведенные в основном здесь расчетные модели не полностью учитывают ряд факторов, влияющих на функционирование трибосистемы. Это прежде всего учет зависимости вязкости и проницаемости пористого слоя от давления; образование промежуточных слоев смазки разной вязкости.
Ниже приведем расчетную модель с учетом зависимости вязкости и проницаемости пористого слоя от давления трехслойной смазки радиального подшипника, обладающего повышенной несущей способностью и демпфирующими свойствами.
Постановка задачи. Рассматривается установившееся стратифицированное течение трехслойной смазки в зазоре радиального подшипника с адаптированным профилем опорной поверхности при наличии пористого слоя на рабочей поверхности вала. Предполагается, что пространство между подшипником и валом полностью заполнено трехслойной вязкой несжимаемой жидкостью. Вал вращается с угловой скоростью W, а подшипник неподвижен. Также предполагается, что зависимость вязкости и коэффициента проницаемости пористого слоя от давления выражается формулами:
(1)
Здесь 
экспериментальная постоянная; 
характерные значения динамического коэффициента смазочных слоев; 
проницаемость пористого слоя; 
гидродинамическое давление.
В полярной системе координат с полюсом в центре вала уравнение адаптированного контура опорной поверхности подшипника, границы раздела слоев и кругового шипа с пористым слоем на его рабочей поверхности можно записать в виде (рис. 1)
(2)
где 
H – толщина пористого слоя.
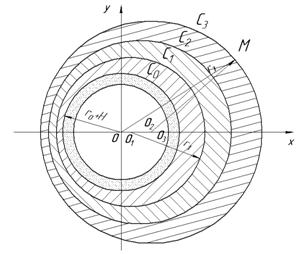
Рис. 1. Схематическое изображение шипа с пористым слоем на его рабочей поверхности в радиальном подшипнике, работающего на трехслойной смазочной композиции
Основные уравнения и граничные условия
В качестве исходных уравнений берутся безразмерная система уравнении движения вязкой несжимаемой жидкости с учетом вязкости от давления для случая «тонкого слоя», уравнение неразрывности, а также уравнение Дарси с учетом зависимости проницаемости от давления
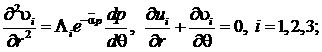
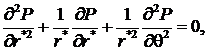(3)
где размерные величины 
в смазочном слое связаны с безразмерными соотношениями
(4)
В пористом слое переход к безразмерным переменным осуществлен по формулам
(5)
Здесь 
– компоненты вектора скорости; 
– характерное давление.
Система уравнений (3) решается при следующих граничных условиях:
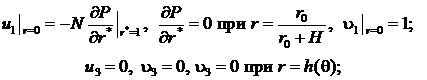
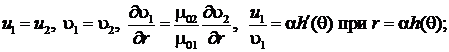
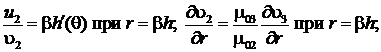
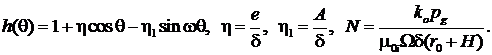(6)
Точное автомодельное решение задачи
Уравнение Дарси осредним по толщине смазочного слоя
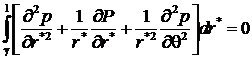(7)
и точное автомодельное решение системы уравнений (3), удовлетворяющее граничным условиям (6), будем искать в виде
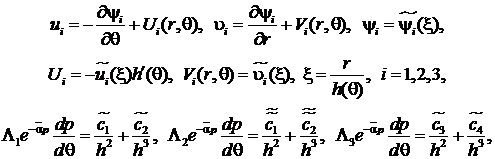
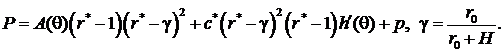(8)
Подставляя (8) в (3) и (6), будем иметь
, (9)
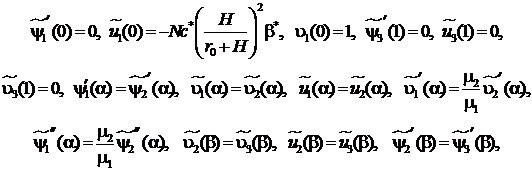
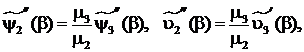
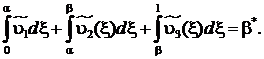(10)
Решение задачи (9) – (10) находится непосредственным интегрированием. В результате будем иметь
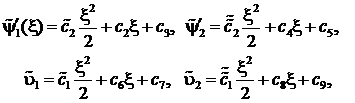
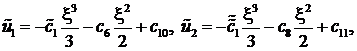
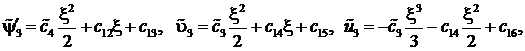
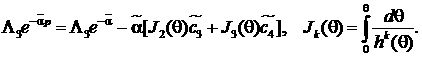(11)
Для определения постоянных 
придем к следующей алгебраической системе уравнений:
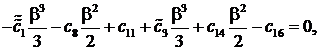
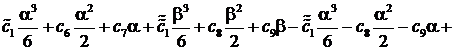
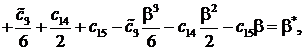
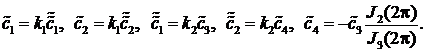(12)
Здесь 
Решение системы (12) сводится к решению следующего матричного уравнения:
(13)
где 
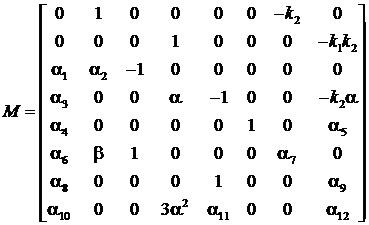. (14)
Здесь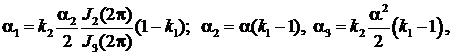 
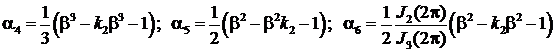
(15)
Решая матричное уравнение (13), получим:
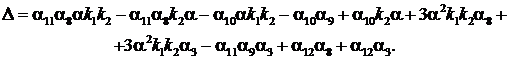(16)
Значения других констант, входящих в систему (13), ввиду громоздкости их выражений здесь не приводятся. Перейдём к определению основных рабочих характеристик подшипника.
Определение гидродинамического давления и основных рабочих характеристик подшипника
В принятом нами приближении для гидродинамического давления получим выражения, аналогичные (10). Безразмерные расходы 
трехслойной смазочной жидкости определяются выражениями
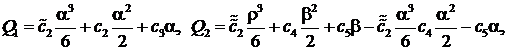
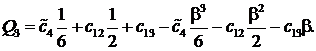
Для безразмерных компонент поддерживающей силы и безразмерного момента трения, получим выражения:
,
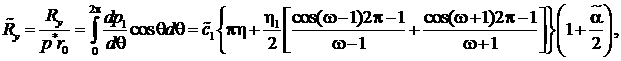
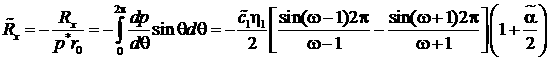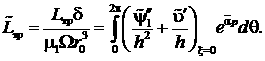(17)
Основные выводы
Результаты численного анализа, приведенные на рис. 2–3, показывают:
1 Безразмерная 
– составляющая вектора поддерживающей силы – существенно зависит от параметра 
, 
и 
.
2 При значениях 
, близких к единице, с увеличением значения вязкостного отношения 
несущая способность возрастает. Наиболее резкое возрастание несущей способности достигается при 
3 При 
, 
наличие пористого слоя на рабочей поверхности вала способствует существенному снижению значения силы трения подшипника, при этом практически не влияет на его несущую способность, в этом случае подшипник обладает повышенной несущей способностью и минимальной силой трения.
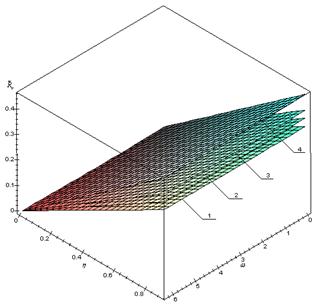
Рис. 2. Зависимость безразмерной несущей способности 
от параметров 
и 
, 
:
1 – 
; 
; 2 – 
; 
;
3 – 
; 
; 4 – 
; 
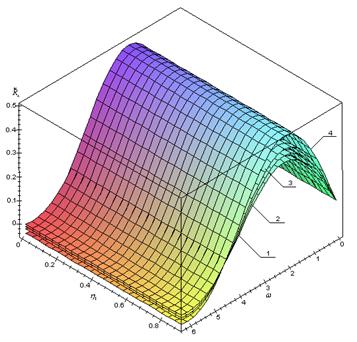
Рис. 3. Зависимость безразмерной несущей способности 
от параметров 
и 
, 
:
1 – 
; 
; 2 – 
; 
;
3 – 
; 
; 4 – 
; 
Литература:
1. Коровчинский М.В. Теоретические основы работы подшипников скольжения. [Текст] М.: Машгиз, 1959, 404 с.
2. Ахвердиев К.С., Приходько В.М., Шевченко А.И., Казанчян О.Р. Математическая модель течения смазки в зазоре радиального подшипника конечной длины со слоистым пористым вкладышем переменной толщины [Текст] // Проблемы машиностроения. РАН М.: Наука - 2000 г. - № 6, - С. 85 – 91.
3. Ахвердиев К.С., Прянишникова Л.И., Пустовойт Ю.И. Гидродинамический расчет пористых подшипников с переменной проницаемостью вдоль оси с учетом нелинейных факторов. [Текст] // Трение и износ. – 1993 - Т. 14, № 5, - С. 813-821.
4. Савенкова С.С. Изучение несущей способности пористого подшипника – [Текст] // Изв. Сев.-Кавк. науч. Центра высш. школы. Сер. Техн. Науки - 1975 г. - № 3, - С. 56-57.
5. Дерлугян Ф.П., Щербаков И.Н. Обоснование процесса получения композиционных антифрикционных самосмазывающихся материалов с заданными техническими характеристиками методом химического наноконструирования. [Электронный ресурс] // «Инженерный вестник Дона», 2010 г., №4 – Режим доступа: http://ivdon.ru/magazine/archive/n4y2010/287 (доступ свободный) – Загл. с экрана. – Яз. рус.
6. Ахвердиев К.С., Прянишникова Л.И. Об одном точном решении задачи о радиальном пористом подшипнике конечной длины [Текст] // Трение и износ. - 1993. - Т. 12, № 1, – С. 24-32.
7. Конри К., Кузано К. Об устойчивости пористых радиальных подшипников [Текст] // Конструирование и технология машиностроения. - 1974. - № 2. – С. 206-216.
8. Ахвердиев К.С., Муленко О.В. Об устойчивости двухслойных пористых радиальных подшипников [Текст] // Вестник РГУПС. - 2002. - № 3.– С. 5-7.
9. Ахвердиев К.С. Мукутадзе М.А., Задорожная Н.С., Флек Б.М., Поляков Е.В., Расчетная модель гидродинамической смазки неоднородного пористого подшипника конечной длины, работающего в устойчивом нестационарном режиме трения при наличии принудительной подачи смазки [Электронный ресурс] // «Инженерный вестник Дона», 2013 г., № 3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2013/1765 (доступ свободный) - Загл. С экрана. – Яз. Рус.
10. Gear C.W., Numarical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall, Inc., Englewood Cliffs. - N.J., 1972.
11. Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamp Towers experiments / O. Reynolds. – Phil. Trans. Roy. Soc. - London, 1886, vol. 177, pt. 1.