Методика теоретико-игрового обоснования условий проведения конкурса

Аннотация

Ю. Н. Макаров, А.А. Строцев

  Предложена методика построения двухуровневой теоретико-игровой модели  конкурса. Задача решается с точки зрения организаторов. Используется комплексный критерий, включающий рейтинг заявки и вероятность выполнения контракта.

Ключевые слова: теоретико-игровая оптимизация, матричные игры, теоретико-игровая модель конкурса

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

Важным аспектом любой деятельности государственных и муниципальных субъектов является организация и проведение конкурсов на поставки товаров, выполнение работ, оказание услуг. Следует отметить, что применяемое законодательство очень сильно зависит от типа проводимого конкурса и объекта закупок. Фактически общими обязательными актами являются Гражданский и Бюджетный кодекс Российской Федерации, а также Федеральный закон Российской Федерации от 21 июля 2005 г. № 94-ФЗ «О размещении заказов на поставки товаров, выполнение работ, оказание услуг для государственных и муниципальных нужд» (ФЗ РФ № 94-ФЗ) [1].  Кроме федеральных законов, регулирующих отношения, связанные с размещением заказов, Правительство РФ приняло ряд нормативных правовых актов.
В соответствие с ФЗ РФ № 94-ФЗ стороны конфликта представлены заказчиком (заказчиками), специализированной организацией, конкурсной комиссией, участниками размещения заказа и поставщиками (исполнителями, подрядчиками).
В качестве заказчиков (государственных или муниципальных) могут выступать соответственно органы государственной власти Российской Федерации или органы государственной власти субъектов Российской Федерации и органы местного самоуправления, а также уполномоченные указанными органами государственной власти или органами местного самоуправления на размещение заказов получатели бюджетных средств при размещении заказов на поставки товаров, выполнение работ, оказание услуг за счет бюджетных средств (далее – уполномоченные органы).
Заказчик или уполномоченный орган (в случае, если такое право предусмотрено решением о создании уполномоченного органа) вправе привлечь на основе договора юридическое лицо (далее – специализированная организация) для осуществления функций по размещению заказа путем проведения торгов в форме конкурса на право заключить государственный или муниципальный контракт (далее также – конкурс) – разработки конкурсной документации, опубликования и размещения извещения о проведении открытого конкурса, направления приглашений принять участие в закрытом конкурсе и иных связанных с обеспечением проведения торгов функций. При этом создание комиссии по размещению заказа, определение начальной цены государственного или муниципального контракта, предмета и существенных условий государственного или муниципального контракта, утверждение проекта контракта, конкурсной документации, определение условий торгов и их изменение осуществляются заказчиком, уполномоченным органом, а подписание государственного или муниципального контракта осуществляется заказчиком.
Поскольку в процессе реализации заказа возможно действие неопределённых факторов, то оценка их действия на результаты размещения заказа имеет важное значение. Учёт неопределённых факторов, не связанных непосредственно с участниками конкурса является отличительным признаком от рассмотренной, например, в работе [2], постановки задачи. В связи с этим исследование различных вариантов порядка и условий проведения конкурсов с обеспечением некоторого принципа справедливости при действии неопределённых внешних факторов является актуальной задачей.
Будем использовать следующие термины: Заказчик (или ЛПР) и Участник конкурса (или Субъект). При этом под Заказчиком (ЛПР) будем понимать субъекты, определяемые понятиями: «заказчик»,  «уполномоченный орган», «специализированная организация», «комиссия по размещению заказа» («конкурсная комиссия»), а под Участником конкурса (Субъектом) – «участника размещения заказа», «поставщика», «исполнителя», «подрядчика», …).
Действия Заказчиков определяется термином «размещение заказа», суть которого заключается в определении по результатам проведения конкурса Субъектов (по представленным ими заявками на участие в конкурсе) в целях заключения контракта на поставки товаров, выполнение работ, оказание услуг для государственных или муниципальных нужд (далее для определённости – выполнение работ).
Построим модель конфликта участников конкурса, с содержанием, описываемым следующими условиями.
1. Описание сторон конфликта участников конкурса.
Число непосредственных участников конкурса – число субъектов , где   – множество Субъектов,  – обозначение мощности множества. В качестве  рассматривается Заказчик или ЛПР.  При этом, как правило, следует учесть действия внешней среды, не имеющей субъектной сущности – природы (). Тогда множество заинтересованных сторон , и, следовательно, в общем случае число сторон конфликта .
2. Описание возможных действий сторон конфликта.
Этап 1. Каждый -й Участник конкурса (Субъект) представляет на конкурс заявку на участие, которая характеризуется набором параметров . Примерами таких параметров могут быть стоимость, время выполнения, квалификация и число непосредственных исполнителей и др. В процессе формирования предложений Участники конкурса формируют свои предложения другим участникам по возможному частичному выполнению работ по заданию в качестве соисполнителей.
Этап 2. ЛПР рассматривает поступившие предложения, оценивает их (пока без учёта возможных действий со стороны ) и выбирает победителя.
Этап 3. Победитель по своему усмотрению и возможностям самостоятельно может взять в соисполнители других Участников конкурса (на условиях согласованных в процессе формирования конкурсных предложений).
Однако ЛПР и Субъектам-участникам конкурса необходимо учитывать действия внешней среды. Различная априорная оценка этих действий приводит к общему снижению реальных результатов исполнения конкурса по сравнению с ожидаемыми (планируемыми).
При существенном отклонении внешних условий (т.е. при наступлении непредсказуемого события (событий), не зависящего от действий исполнителя контракта по конкурсу, но ведущее к невозможности исполнения договорных обязательств) исполнитель может требовать расторжения контракта или упрощение условий его выполнения.  Отметим, что к таким (форс-мажорным) обстоятельствам не относятся события, порождённые коммерческим риском (например, изменение цены, неблагоприятная конъюнктура, …).
Поскольку в результате действия таких фактором могут возникать спорные вопросы, то для их избегания в конкурсной документации следует описывать рамки основных действующих внешних факторов.
3. Ограничения проблемной ситуации:
– одношаговость процедуры (для Субъектов);
– Субъекты – участники конкурса не образуют коалиции и не обмениваются информацией о поданных предложениях, но могут уточнять предложения об участии других сторон в реализации выигранного контракта;
– конкурс может быть признан состоявшимся только при числе участников конкурса не менее двух (в соответствие с ФЗ РФ № 94-ФЗ участник конкурса может быть и один, но при построении теоретико-игровой модели необходимо, чтобы число участников было не менее двух);
– ЛПР устанавливает правила проведения конкурса, доводит их до участников конкурса и следит за соблюдением этих правил.
Построение модели игры будем проводить путём формирования её частных моделей.

Общая информация по конкурсу.
Пусть проводится конкурс по результатам которого ЛПР требуется выбрать Участника конкурса (Субъекта) для разработки и построения сложной технической системы (СТС). По условиям конкурса заявки оцениваются по L показателям. При этом, поскольку стоимость контракта имеет важное значение как показатель оценки заявки, то закрепим за этим показателем индекс (номер) L.

Модель формирования стратегий ЛПР по определению требований к СТС в рамках конкурса.
Ограничимся следующим порядком формирования стратегий ЛПР, представляющих собой наборы задаваемых предельных значений этих показателей (в условных единицах):
,
, , ,
, , в общем случае .

Модель формирования Субъектами заявок.
Обозначим через  номер варианта заявки Субъекта (номер его стратегии), где  – число стратегий -го Субъекта. Тогда одним из путей их формирования для i-го набора требований (i-й стратегии ЛПР) является применение выражений вида:
,
,
где ,  – заданные коэффициенты, улучшающие значения величин показателей, определённых условиями конкурса, ;  для показателей, большие значение которых предпочтительнее меньших;   для показателей, меньшие значение которых предпочтительнее больших; 
 – предельное значение показателя, обусловленное его смыслом (например, для -го показателя, который по смыслу является вероятностью наступления случайного события ).
Примеры формирования стратегий на основе только первого и второго способа соответственно:
.

.

Оценочная функция заявки (рейтинг заявки).
Рассмотрим следующий вид оценочной функции заявки, определяемой значениями показателей :
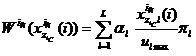,                                                    (1)
где  – максимальное значение l-го показателя среди элементов множества  (рассматривается как нормирующий коэффициент в функции свёртки векторного предпочтения);      – весовой коэффициент l-го показателя в функции свёртки векторного предпочтения, ,  для показателей с номером l, оцениваемых ЛПР в категории «чем больше, тем лучше»,  для показателей с номером l, оцениваемых ЛПР в категории «чем меньше, тем лучше».

Модель неопределённых факторов, влияющих на выполнение работ по контракту.
Поскольку на результаты выполнения работ по конкурсу могут оказывать влияние неопределённые факторы, рассмотрим одну из возможных моделей их учёта. Положим число этих факторов (их значений) конечным и равным J. Обозначим эти факторы в виде набора  несовместных событий, одно из которых обязательно произойдёт. Ограничимся учётом влияния этих факторов на получаемую Субъектами экономическую выгоду от реализации контракта и на вероятность его результативного исполнения Субъектом.

Модель расходов и дохода Субъектов при выполнении работ по контракту.
Без учёта влияния неопределённых факторов расходы на реализацию контракта представим в следующем виде:
,
где
, ,
 – максимальная сумма предложения по контракту из типовых условий, это величина максимального значения элементов множества  (в условиях примера – );
 – коэффициент, характеризующий часть от величины , выделяемую для развития; при этом полагается, что средств  достаточно, чтобы выполнить условия контракта при заданном наборе требований;
,  – минимальное значение среди элементов множества  ;
 – коэффициент, характеризующий долю средств, планируемую для выполнения требований контракта по l-му показателю, ;
 – коэффициент, характеризующий долю средств, планируемую на постоянные расходы для выполнения требований контракта;
 – коэффициент, степень увеличения доли средств, необходимой для выполнения требований контракта по l-му показателю при улучшении значения l-го показателя относительно величины , ;
 – значение l-го показателя эффективности представленного в заявке -го Субъекта на участие в конкурсе,  (в условиях примера );
Уточним представленную модель в условиях действия j-го неопределённого фактора :
,                           (2)
где ,  – коэффициенты увеличивающие расходы Субъекта при  действии j-го неопределённого фактора (,,).
Доход при выполнении работ по контракту для -го Субъекта при действии j-го неопределённого фактора определяется по выражению:
.                                                 (3)

Вероятность выполнения контракта по заданным условиям и действиям неопределённых факторов.
При формировании модели оценки вероятности выполнения контракта по заданным условиям и действиям неопределённых факторов учтём её зависимость от дохода Субъектов. Тогда эта вероятность для  -го варианта заявки -го Субъекта может быть определена по выражению
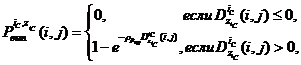                                         (4)

где коэффициент  определяется как решение уравнения  при заданных значениях , , т.е. .

Теоретико-игровая модель поведения Субъектов.
Теоретико-игровые модели отношений между Субъектами в конкурсе могут быть различными. Одним из достаточно общих возможных подходов является решение в смешанных стратегиях. Тогда множества смешанных стратегий игроков принимают вид: 
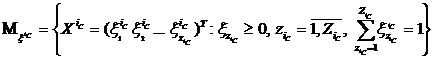,                  (5)
В результате решения игры формируются оптимальные смешанные стратегии , для которых получаемое решение игоков-Субъектов для различных условий конкурса и значений неопределённого фактора выражается в значениях дохода или в значениях его математического ожидания. Обозначим это решение в виде . Для мета-игры результаты разыгрываний представляют комплексный результат, выраженный в значениях:
– показателей, характеризующих рейтинг (как степени достижения цели конкурса) ;
– вероятностей выполнения контракта при заданных условиях проведения конкурса и значений неопределённого фактора  как функции от .
Ограничимся случаем, когда . Тогда, поскольку число стратегий игроков конечно, а число самих игроков равно двум, то предпочтения игроков может быть выражено на основе построения матриц игры для каждого игрока при фиксированных индексах i и j:
, , , .                     (6)
Исходными данными для их заполнения являются значения дохода при выполнении работ по контракту для -го Субъекта при действии j-го неопределённого фактора и i-го варианта условий, сформированных ЛПР:
, .                                            (7)
Доход Субъекта отличен от нуля, если рейтинг его заявки (предложения) выше (не ниже), соответствующего рейтинга конкурирующего Субъекта, т.е.:
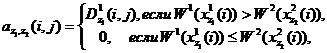                               (8)
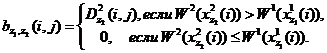                              (9)
При выполнении равенства  возникает ситуация неопределённости, разрешение которой возможно на основе конкурсных правил (например, вида: «контракт в этом случае получает Субъект, заявка которого поступила на рассмотрение первой»).
Выражения (8), (9) определяют конечное число вариантов заполнения матриц , : 
1) , ;
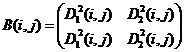2) , ;
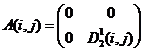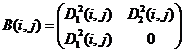3) , ;
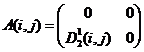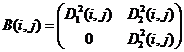4) , ;
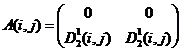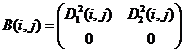5) , ;
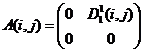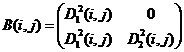6) , ;
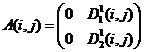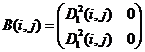7) , ;
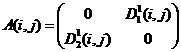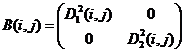8) , ;
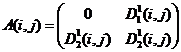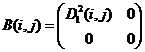9) , ;
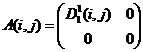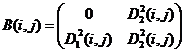10) , ;
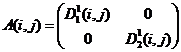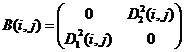11) , ;
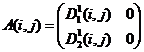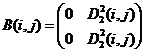12) , ;
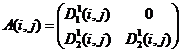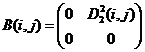13) , ;
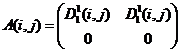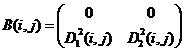14) , ;
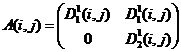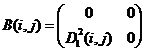15) , ;
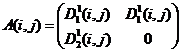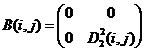16) , .
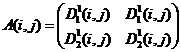Варианты 1 – 6, 8, 9, 11 – 16 дают решение в чистых стратегиях игроков (Субъектов), а 7 и 10 – в смешанных (индексы i, j опущены):
,,                                 (10)
,                          (11)
.                         (12)
При этом решение биматричных игр может быть получено по выражениям (см., например, [3], с. 135):
,                                                 (13)
,                                                 (14)
где , , , , – невырожденные матрицы.             
Решения для игоков-Субъектов для вариантов 1 – 6, 8, 9, 11 – 16 выражаются в значениях дохода, а для  вариантов 7 и 10 – в значениях их математических ожиданиях.

Модель мета-игры в системе «ЛПР – Природа».
Осуществляя свёртку по показателям  и  получим значения элементов матрицы мета-игры :
,                                                 (15)
где  – заданная функция свёртки.
Поскольку в играх с Природой интересы игроков полагаются противоположными, то  в результате получим одну из форм моделей матричных игр с нулевой суммой, представленных в монографии [4].

Описанные действия по формированию полученных выше моделей, решению частных задач и реализации полученных решений можно рассматривать в качестве методики теоретико-игрового обоснования условий проведения конкурса.

Рассмотрим пример.
Пусть число показателей оценки заявок равно пяти (L=5), а сами показатели определены категориями надёжность, эффективность системы, срок выполнения, квалификация исполнителей и стоимость контракта, т.е. , соответственно.
Тогда , где – множества с конечным числом элементов, причём: , , , , .
Пусть значения элементов множеств  и  характеризуют соответствующие показатели как часть от нормативных величин, т.е. являются коэффициентами. При этом элементы множества , с большими значениями характеризуют меньшее допустимое время выполнения контракта, т.е.  рассматривается как множество коэффициентов сокращения нормативных сроков (нормативный срок делится на эти коэффициенты).
Большие значения элементов множеств – соответствуют более жёстким требованиям в условиях контракта.
Для исследования структуры предлагаемых заявок рассмотрим две модели. Первую условно определим как модель, ориентированную на улучшение показателей кадрового обеспечения выполнения контракта (4-го) и стоимости выполнения контракта (5-го), а вторую – надёжности и эффективности (1-го и 2-го, соответственно).
Ограничимся в рамках примера числом возможных стратегий Субъектов равным двум и положим



с заданными значениями коэффициентов , :

при .
В модели оценочной функции заявки выберем:

В условиях примера рассмотрим три группы учитываемых неопределённых факторов, характеризующих риски: увеличения постоянных расходов (), удорожания технических компонентов СТС () и повышения расходов на привлечение квалифицированного персонала ().
В модели расходов и дохода Субъектов при выполнении работ по контракту определим следующие значения констант:
 – максимальная сумма предложения по контракту из типовых условий, это величина максимального значения элементов множества  , ;;

              , , т.е. .

              Получим решение задачи.
Для этого определим число потенциально возможных стратегий ЛПР: . Для обозримого примера ограничимся тремя стратегиями, представленными в виде следующей таблицы:

              Используя данные этой таблицы можно сформировать стратегии Субъектов – заявки на участие в конкурсе и оценить их рейтинг по выражению (1):

В условиях действия неопределённых факторов значения расходов Субъектов, их доходов и вероятностей выполнения контрактов, определяемых по выражениям (2) – (4) соответственно, представлены в следующей таблице:

Отрицательные значения  позволяют сократить число рассматриваемых стратегий ЛПР. В частности первая стратегия является неприемлемой для него.
Заполним матрицы игры для ситуаций  
1) , ;
2) , ;
3) , ;
4) , ;
5) , ;
6) ,
и определим решения, записывая результат в таблицу

Её анализ (как мета-игры в системе «ЛПР – Природа») позволяет сделать вывод о том, что ЛПР следует организовать конкурс с условиями, соответствующими его третьей из рассмотренных стратегий:

              При этом будет обеспечен наивысший рейтинг с вероятностью выполнения условий контракта равной 1.

              Выводы:
1. Разработанная методика теоретико-игрового обоснования условий проведения конкурса позволяет при оценке возможных действий неопределённых факторов определить наилучшие для ЛПР условия по двум показателям: обобщённому рейтингу и вероятности выполнения контракта.
2. Основное отличие от известных подходов, использующих теоретико-игровые модели при реализации конкурсов, разработанная методика основана на построении  мета-игры в системе «ЛПР – Природа», исходные данные для которой формируются на уровне игровой ситуации с игроками-участниками конкурса.
3. Рассмотренный демонстрационный пример подтвердил работоспособность представленной методики.

Литература
1. Федеральный закон Российской Федерации от 21 июля 2005 г. № 94-ФЗ.
2. Мазалов В.В., Токарева Ю.С. Теоретико-игровые модели проведения конкурсов // Математическая теория игр и её приложения, 2010. – т.2. – в.2. – С. 66–78.
3. Петросян Л.А., Зенкевич Н.А., Сёмина Е.А. Теория игр. – М.: Высш. шк., Книжный дом «Университет», 1998.
4. Макаров Ю.Н., Строцев А.А. Методология исследования сложных организационно-технических систем, функционирующих в конкурентной среде при ограниченных ресурсах. Ростов-на-Дону, 2010.