Особенности динамического возбуждения слоистых сред внутренними источниками колебаний
Аннотация
Рассмотрены особенности построения эффективных решений в задачах возбуждения многослойных сред внутренними источниками колебаний. Приведены примеры численных расчетов перемещений и напряжений в среде в зависимости от положения источника и точки наблюдения.
Ключевые слова: многослойное основание, внутренний источник, гармонические колебания
Задачи расчета поверхностных сооружений при динамических воздействиях внутренними источниками колебаний связаны с проблемами сейсмостойкого строительства, возведением зданий в зонах, близких к линиям метрополитена мелкого и среднего заложения. При этом основные особенности такого воздействия связаны как со спектральным составом возбуждения, так и строением неоднородного грунта. Во многих случаях грунт можно моделировать слоисто–неоднородной упругой или вязкоупругой средой.
1. Постановка задачи
Рассматривается задача возбуждения гармонических колебаний внутренним источником, заглубленным в слоисто-неоднородную полуплоскость.
Пусть область, занимаемая линейно-упругой средой представляет собой многослойную полуплоскость 
(Рис. 1).
- полуплоскость;
-j-й слой (j=2,...,N);
Рис. 1
Физические свойства среды описываются плотностью 
и скоростями распространения поперечных и продольных волн: 
.
Условия стыковки разнородных сред считаются жесткими с требованием непрерывности векторов перемещений и напряжений при переходе через границы раздела.
В точке с координатами 
действует сосредоточенный источник гармонических с частотой 
колебаний:
2. Построение решения
Решение поставленной задачи соответствует построению матрицы фундаментальных решений точечного источника, реализация которого осуществляется с помощью принципа суперпозиции.
В основе данного построения решения для многослойной среды лежит вывод определяющих соотношений для одного слоя с заданными на его гранях векторами напряжений.
Пусть в локальной системе координат для 
-го слоя: 
амплитудные функции перемещений при действии сосредоточенного в 
источника имеют вид:
.
Функции 
удовлетворяют уравнениям движения Ляме [1]
,
и 
- постоянные Ляме: 
, 
.
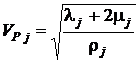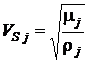Согласно предлагаемому методу данные функции будем разыскивать в виде
.
(При аналогичном рассмотрении полуплоскости считаем 
).
Здесь слагаемые 
данного представления являются решениями уравнений Ламе для однородной полуплоскости с удовлетворением граничных условий:
, 
.
Вектор перемещений 
представим в виде интеграла Фурье через трансформанты вектора напряжений 
:
. (1)
Контур 
определен принципом предельного поглощения: обходит положительные полюса подынтегральной функции снизу, отрицательные - сверху, а на остальной части совпадает с вещественной осью. Элементы матрицы 
имеют вид:
, 
,
, 
,
, 
,
,
- скорости распространения волн в соответствующей среде.
Аналогично формуле (1) определяются перемещения для полуплоскости 
через функции 
, где для элементов 
справедливы соотношения:
, 
, 
- символ Кронекера.
Определяя напряженное состояние слоя в виде суммы соответствующих решений для двух полуплоскостей, получим:
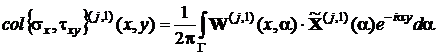, (2)
где
, 
,
, 
.
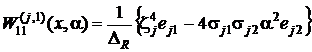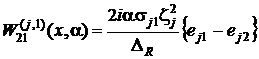Для второй группы слагаемых найдем:
.
Соответственно функции 
определяют перемещения в однородной плоскости с параметрами рассматриваемого слоя от действия сосредоточенного источника колебаний 
в виде набора цилиндрических волн [2] и соответствуют компонентам матрицы 
:
.
С помощью формул переразложения [3] они могут быть записаны в преобразованном по Фурье виде:
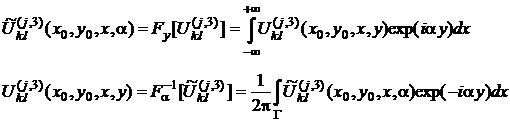, k,l=1,2,
где
,
,
,
.
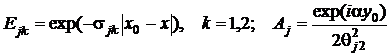Аналогично для фундаментальных решений по напряжениям получим:
.
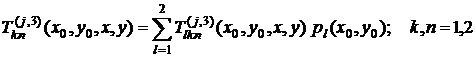Или в преобразованиях Фурье:
, 
,
,
,
.
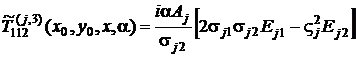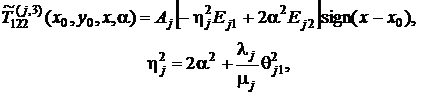
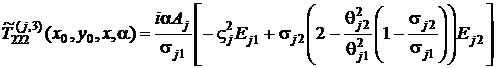Введенные трансформанты Фурье функций напряжений 
представлений (1), (2) являются неизвестными и должны быть определены из условий стыковки разнородных составляющих слоистой полуплоскости между собой. Удовлетворяя равенствам компонент векторов перемещений и напряжений при переходе через границы раздела сред в преобразованиях Фурье, получим систему линейных алгебраических уравнений с 
неизвестными:
,
где 
- общий вектор неизвестных напряжений для многослойной структуры.
Полученные таким образом фундаментальные решения обладают важным свойством отсутствия напряжений на дневной поверхности 
.
- Анализ численных результатов
В качестве иллюстрации характера поведения построенных фундаментальных решений исследованы зависимости компонент вектора перемещений и тензора напряжений от положения источника, точки наблюдения и свойств слоев полуплоскости.
На рис. 2 показано поведение нормальных вертикальных напряжений 
в зависимости от положения источника колебаний в фиксированной точки наблюдения (с координатами (-5; 0,5)). Положение источника определяется выражением 
, 
. По анализу графика видно, что в точке наблюдения развиваются интенсивные колебания, при положении источника внутри слоя пониженной жесткости, имеющие немонотонный характер. Максимальное значение данных напряжений превышает уровень напряжений при возбуждении среды с поверхности более чем в 10 раз.
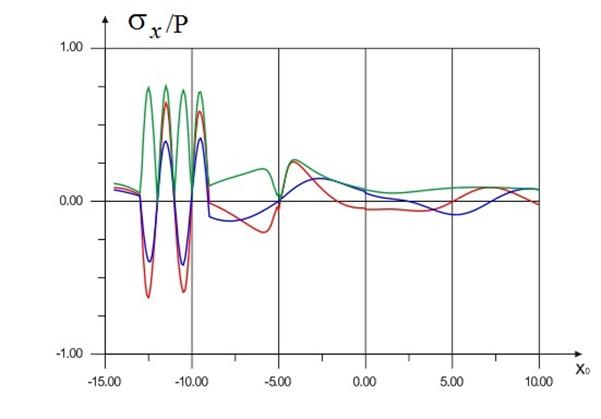
Рис. 2
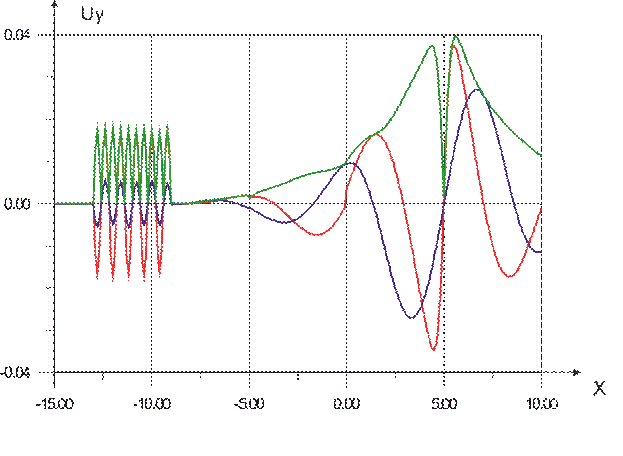Рис. 3
На рис. 3 представлены горизонтальные перемещения 
, в случае возбужения среды внутренним источником колебаний, расположенном на глубине x0=5 в полуплоскости. При движении точки наблюдения от поверхности среды х = -15 в глубь х=10. Мягкая прослойка, положение которой определяется диапазоном 
приводит к экранированию горизонтальных смещений выше нее. В самой же прослойке наблюдаются осциллирующие на глубине колебания, соизмеримые с колебаниями вблизи источника, которые имеют более плавный характер, по отношению к точке наблюдения.
Имеющие общие закономерности, особенности поведения напряжения состояния среды, наблюдается так же в случае наличия более жесткой прослойки, а также в сочетании жесткая - мягкая прослойка. Таким образом, структура слоистой конструкции существ образом влияет на характер волновых полей, генерируемых внутренним источником колебанием, при наблюдении, как на поверхности области, так и внутри нее.
ЛИТЕРАТУРА
1.Новацкий В. Теория упругости. М.: Мир, 1975. –872 с.
2.Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. -М.: Мир, 1984.
3.Морс Ф.М., Фешбах Г.Методы теоретической физики. -Т.1. М.: Изд-во иностр. лит., 1958. –930 с., -Т.2. М.: Изд-во иностр. лит., 1960. –886 с.