Свойство инерционности в изучении проблемы управления социально-экономическими процессами рынка труда

Аннотация

М.П. Муравьева

Дата поступления статьи: 25.08.2013

В статье рассматривается  математическая формализация  понятия инерционности системы в целом, и в частности инерционности социально-экономической системы, возникающей при изучении процессов и явлений рынка труда. Данное свойство позволяет учесть проблему временного разрыва между управляющим воздействием и результатом изменения системы  рынка труда на данное воздействие.

Ключевые слова: Рынок труда, инерционность, экономико-математическое моделирование, управляющее воздействие, социально-экономическая система

08.00.05 - Экономика и управление народным хозяйством (по отраслям и сферам деятельности)

Специфика проблемы управления социально-экономическими процессами рынка труда, вызывает необходимость разработки экономико-математических моделей, позволяющих расширить аппарат исследования и инструментарий выработки и принятия оптимальных решений, учитывающих динамичность изменения экономической ситуации и неполноту исходной информации.
К моделям, выявляющим сущность социально-экономических процессов рынка труда, а также осуществляющим прогноз выходных параметров, относятся, прежде всего, различные эконометрические модели. Этот класс моделей оперируют с численными значениями экономических переменных и позволяют получить их статистически значимые оценки на основе имеющихся наблюдений. С помощью оптимизационных моделей, критерием эффективности которых выступает целевая функция, решаются задачи управления и оптимизации. Данная классификация моделей весьма условна, поскольку все вышеперечисленные задачи могут быть решены и в тех и других моделях в зависимости от целей исследования.
Рынок труда – это сложная социально-экономическая система, при моделировании социально-экономических процессов и явлений которой необходимо учитывать ряд специфических свойств, проявляющихся при исследовании экономических объектов. Характерными свойствами социально-экономических систем являются неопределенность исходных данных, открытость, зашумленность информации, стохастичность объекта, нелинейность, нестационарность, динамичность, уникальность, инерционность [1]. Остановимся подробнее на рассмотрении такого свойства социально-экономической системы, как инерционность. Для технических систем в литературе известно следующее определение данного свойства:
Инерционность – это свойство объекта, характеризующее значение выхода объекта Y в момент времени t, которое зависит не только от значения входа X вэтот же момент времени, но и от всей его предыстории. Объекты принято считать динамическими, если вход и выход инерционного объекта являются функциями, зависящими от времени.
Интегралом свертки (Дюмеля) описываются инерционные объекты в простейшем случае (линейном, стационарном) [2,3,4]:
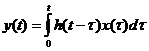(1)
Здесь  - переменная интегрирования, изменяющаяся согласно (1) в пределах от 0 до t. При этом вход пробегает все значения от x(0) до последнего x(t). Эти значения «суммируются» с весом h(t-h). В случае нестационарности объекта, весовая функция h будетзависит не только от разностиt-h, но и от t, то есть получим функцию h (t, t-τ).
В случае нелинейных инерционных объектов используется обобщение (1), которое называется полиномом (при ограниченном числе слагаемых), рядом (в противном случае) Вольтера.
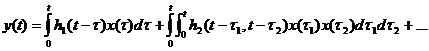(2)
Полагая в (1) и в (2) , что весовая функция , где δ – функция, определяется соотношениями:


Получим, что (1) и (2) представляют собой соответственно линейный и нелинейный (степенной) полином (ряд):
(3)
(4)
Соотношение (3) используется для линейных, стационарных, динамических, детерминированных объектов. Соотношение (4) аналогично свойствам объекта в уравнении (3), однако учитывает нелинейную зависимость. В случае нестационарности объектов коэффициенты h в формулах (3) и (4) являются функциями времени.
Вернемся к рассмотрению свойства инерционности для социально – экономической системы рынка труда. Инерционность,которая характеризует все объекты и системы окружающего мира, в том числе и социально-экономические системы, подразумевает, что системе требуется некоторое время для изменения состояния и скорости развития после приложенных к ней управляющих воздействий. Из двух систем, более инерционной считается та система, которая медленнее изменяет свое состояние при одинаковых воздействиях [5,6].
Высокая инерционность может проявляться в качестве положительного свойства, в случае слабой чувствительности объекта управления к внешним возмущающим воздействиям (сохранение его устойчивости), и в качестве отрицательного, демонстрируя нечувствительность (невосприимчивость) к внешним воздействиям.Малой инерционности объекта исследования также характерны положительные (высокая управляемость) и отрицательные (реагирование на случайные возмущения) свойства системы [5,7].
В научной литературе по экономике и менеджменту уже встречается понятие «инерционности» социально-экономической системы в математическом описании изменения интенсивности V(t) выпуска предприятием конечного продукта [5,8]:
,   (5)
здесь - показатель, характеризующий прирост интенсивности выпуска конечного продукта размерностью – [руб/время²]; G(t) – величина, определяющая интенсивность капитальных вложений в производство, размерностью – [руб/время]; а вводимый показатель , имеющий размерность [время], характеризует в данном случае «инерционность» исследуемой экономической системы.
Рассмотренное выше уравнение описывает экономический процесс аналогично уравнению физического процесса движения материального тела с постоянной массой , которое перемещается с ускорением  под воздействием силы G(t), зависящей от времени [9,10]. Для нашей экономической системы это значит, что, если в качестве  рассмотрим, например, промежуток времени равный два года, то капитальные вложения, характеризующиеся интенсивностью G(t) равной1 руб/год могут обеспечить годовой прирост интенсивности выпуска конечного продукта  на 0,5 руб/год. Данный пример характеризует «инерционность» социально-экономической системы как параметр, имеющий размерность – [время].
Рассмотренное свойство инерционности также, как и остальные характеристики социально-экономических систем, усложняют процесс моделирования, однако их необходимо постоянно учитывать на всех этапах построения экономико - математических моделей, начиная с выбора вида модели и заканчивая различными аспектами прикладного использования результатов моделирования. Математическое моделирование социально-экономических систем (объектов или процессов), имеющих сложную внутреннюю структуру, например как рынок труда, которую невозможно математически построить, исходя из физики явления, предполагает использование понятия «черный ящик». Система, где наблюдению доступны лишь входные и выходные величины, а внутреннее устройство ее и процессы, в ней протекающие остаются неизвестными, носит название «черный ящик» [7]. Подход, использующий понятие «черный ящик» находит широкое применение в исследовании сложных социально-экономических систем в том случае, когда необходимо знание поведения системы, а не ее строение.

Литература:

1. Муравьева М.П. Принципы оптимальности в изучении социально-экономических процессов рынка труда// «Инженерный вестник дона» 2012 №4 (часть 2) – Режим доступа: http:// www.ivdon. Ru /magazine/archive/n4p2y2012/1245(доступ свободный) – Загл. с экрана. – Яз. рус.
2. Лябах Н.Н., Шабельников А.Н. Техническая кибернетика на железнодорожном транспорте: Учебник. Ростов - на - Дону, 2002. - 283с.
3. Berkovitz, L. D. Optimal Control Theory, number 12 in Applied Mathematical Sciences, Springer-Verlag, New York{Heidelberg{Berlin, ISBN 0-387-90106-X, 1974, 304 pp.
4. S.M. Aseev and A.V. Kryazhimskiy, The Pontryagin maximum principle and transversality conditions for a class of optimal control problems with infinite time horizons, SIAM J. on Control and Optimization, 43, pp. 1094–1119, 2004.
5. Солдатова И.А., Муравьева М.П. Оценка эффективности процесса обучения специалистов// Terra Economicus Экономический вестник Ростовского государственного университета. - 2009.- Том 7. - №4 (часть3). - С. 322-325.
6. Чернов, А.В. Методы линеаризации и модели контролируемых нелинейных дискретных динамических систем [Текст]// Научно-технические ведомости Санкт-Петербургского государственного политехнического университета, 2009. - №2. – С. 156-162.
7. Ильичева О.А. Технология логического моделирования и анализа сложных систем// «Инженерный вестник дона» 2012 №4 (часть 2) – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1234(доступ свободный) – Загл. с экрана. – Яз. рус.
8. Кравченко Р.Г., Скрипка А.Г. Основы кибернетики. Учеб. пособие для экон. спец.с.-х. вузов [Текст]. - М: «Экономика», 1974. - 279с.
9. Кобринский Н.Е. и др. Введение в экономическую кибернетику. Учеб. пособие. - М.: «Экономика», 1975. - 343с.
10. Энциклопедия кибернетики. Т. - 1-2. - Киев: УСЭ, 1975. - 607с.; 620с.