Исследование динамики волнового фронта фокусирующего излучателя ультразвука
Аннотация
Проведен анализ поля сферически сходящегося звукового пучка. В качестве параметра, отражающего эволюцию волны, использована кривизна поверхности фронта. Получены выражения, позволяющие определять величину кривизны фазового фронта в звуковых пучках с разными амплитудными распределениями. Приведены осевые и поперечные распределения кривизны фронта в фокусирующем пучке с гауссовым и равномерным распределениями амплитуды. Отмечено качественно разное влияние кривизны поверхности излучателя на динамику волнового фронта в случаях , и . Приведены аналогичные характеристики для плоского
Ключевые слова: Фокусирующий излучатель; дифракция; кривизна фазового фронта
В работе рассматривается подход к определению кривизны фронта в распространяющемся звуковом пучке [1 – 4], который дает количественную оценку происходящей эволюции волны. В общем случае, когда необходимо определить кривизну фронта волны в произвольной точке пространства, воспользуемся понятием кривизны линии [2]. Тогда кривизна фронта волны в пучке запишется
![]() (1)
(1)
где ![]() ,
, ![]() – поперечная и осевая координаты;
– поперечная и осевая координаты; ![]() – пространственное «запаздывание» фазы дифрагирующей волны относительно плоской;
– пространственное «запаздывание» фазы дифрагирующей волны относительно плоской; ![]() . Для эталонного случая в виде гауссового пучка [1, 3] кривизну можно записать:
. Для эталонного случая в виде гауссового пучка [1, 3] кривизну можно записать:
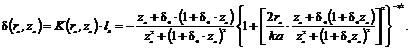 (2)
(2)
Здесь ![]() – безразмерная кривизна фронта;
– безразмерная кривизна фронта; ![]() – радиус кривизны фронта;
– радиус кривизны фронта; ![]() и
и ![]() – нормированные координаты;
– нормированные координаты; ![]() – радиус излучателя;
– радиус излучателя; ![]() – длина области дифракции Френеля;
– длина области дифракции Френеля; ![]() – безразмерная кривизна рабочей поверхности излучателя;
– безразмерная кривизна рабочей поверхности излучателя; ![]() – радиус рабочей поверхности излучателя.
– радиус рабочей поверхности излучателя.
Кривизна фронта в пучке с равномерным амплитудным распределением
![]() (3)
(3)
![]() ,
, ![]() .
.
Функции ![]() ,
, ![]() ,
, ![]() находятся как аргумент комплексной амплитуды волны из решения параболического уравнения дифракции [4].
находятся как аргумент комплексной амплитуды волны из решения параболического уравнения дифракции [4].
Осевые распределения безразмерной кривизны волны ![]() при разных значениях кривизны поверхности излучателя
при разных значениях кривизны поверхности излучателя ![]() приведены на рис. 1. Выделим три качественно разных случая:
приведены на рис. 1. Выделим три качественно разных случая: ![]() ,
, ![]() и
и ![]() , рис.2.
, рис.2.
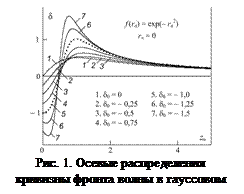
Для плоского излучателя (![]() ) осевое распределение кривизны фронта волны показано кривой 1 на рис. 1 [1,3]. Здесь волна трансформируется из квазиплоской в сферически расходящуюся волну, последовательно проходя этапы
) осевое распределение кривизны фронта волны показано кривой 1 на рис. 1 [1,3]. Здесь волна трансформируется из квазиплоской в сферически расходящуюся волну, последовательно проходя этапы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , рис. 2–а. Вблизи излучателя форма волны (
, рис. 2–а. Вблизи излучателя форма волны (![]() ) плоская. По мере распространения фронт под действием дифракции искривляется (
) плоская. По мере распространения фронт под действием дифракции искривляется (![]() ), достигая на расстоянии
), достигая на расстоянии ![]() максимальной кривизны (
максимальной кривизны (![]() ). С прекращением дифракции (
). С прекращением дифракции (![]() ) волновой фронт распрямляется (этап
) волновой фронт распрямляется (этап ![]() ), стремясь в процессе сферического расхождения волны принять на локальном участке плоскую форму (
), стремясь в процессе сферического расхождения волны принять на локальном участке плоскую форму (![]() ).
).
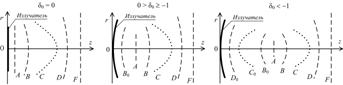
Начальный этап (![]() или
или ![]() ) эволюции волны фокусирующего излучателя (
) эволюции волны фокусирующего излучателя (![]() ) проходит под влиянием геометрической сходимости, рис. 2–(б, в). При этом слабо сходящимся пучкам (
) проходит под влиянием геометрической сходимости, рис. 2–(б, в). При этом слабо сходящимся пучкам (![]() ) свойственно преобладание вклада дифракции над геометрической сходимостью, здесь волна проходит этапы
) свойственно преобладание вклада дифракции над геометрической сходимостью, здесь волна проходит этапы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , рис. 2–б. Функция
, рис. 2–б. Функция ![]() начинается значением
начинается значением ![]() , проходит через нулевое значение со сменой своего знака и по достижении максимума монотонно стремится к нулю, кривые 2 – 5 на рис. 1. Область фокуса пучка совпадает с нулевым значением кривизны, где волна имеет плоский фазовый фронт (
, проходит через нулевое значение со сменой своего знака и по достижении максимума монотонно стремится к нулю, кривые 2 – 5 на рис. 1. Область фокуса пучка совпадает с нулевым значением кривизны, где волна имеет плоский фазовый фронт (![]() ).
).
Сильно сходящиеся пучки (![]() ) отличаются доминированием геометрической сходимости над дифракцией, в результате формируются вогнутый (
) отличаются доминированием геометрической сходимости над дифракцией, в результате формируются вогнутый (![]() ) и выпуклый (
) и выпуклый (![]() ) фронты максимальной кривизны. В функции
) фронты максимальной кривизны. В функции ![]() появляются экстремумы в области отрицательных значений
появляются экстремумы в области отрицательных значений ![]() , кривые 6 и 7, рис. 1. Отметим, что в дальней области пучка (
, кривые 6 и 7, рис. 1. Отметим, что в дальней области пучка (![]() ) зависимости
) зависимости ![]() повторяются для всех
повторяются для всех ![]() , что соответствует изменениям фронта волны
, что соответствует изменениям фронта волны ![]() и
и ![]() , рис. 2–(а–в).
, рис. 2–(а–в).
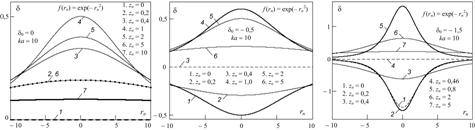
Поперечные распределения кривизны волны ![]() в гауссовых пучках с волновым размером
в гауссовых пучках с волновым размером ![]() = 10 для случаев
= 10 для случаев ![]() ,
, ![]() и
и ![]() показаны на рис. 3. Изменения
показаны на рис. 3. Изменения ![]() демонстрируют отмеченные выше закономерности. Так в случае
демонстрируют отмеченные выше закономерности. Так в случае ![]() этапу сферической расходимости волны предшествует этап нарастания кривизны фронта (
этапу сферической расходимости волны предшествует этап нарастания кривизны фронта (![]() ), кривая 4, рис. 3–а. В отличие от плоского излучателя (
), кривая 4, рис. 3–а. В отличие от плоского излучателя (![]() ), трансформация волны фокусирующего излучателя сопровождается сменой знака кривизны ее фронта. На расстояниях между излучателем и фокусом волна имеет сходящийся фронт, здесь
), трансформация волны фокусирующего излучателя сопровождается сменой знака кривизны ее фронта. На расстояниях между излучателем и фокусом волна имеет сходящийся фронт, здесь ![]() . В точке фокуса, положение которой на оси пучка меняется с величиной
. В точке фокуса, положение которой на оси пучка меняется с величиной ![]() , волна принимает плоский фазовый фронт
, волна принимает плоский фазовый фронт ![]() , кривая 3 на рис. 3–б и кривая 4 на рис. 3–в. За фокусом кривизна фронта становится положительной (
, кривая 3 на рис. 3–б и кривая 4 на рис. 3–в. За фокусом кривизна фронта становится положительной (![]() ), что соответствует расходящейся волне.
), что соответствует расходящейся волне.
 |
||
|
а) |
б) |
в) |
|
Рис. 2. Пространственные изменения формы волны в зависимости от |
||
|
|
||
|
а) |
б) |
в) |
|
Рис. 3. Поперечные распределения кривизны фронта волны в гауссовом пучке |
||
|
|
|
|
а) |
б) |
|
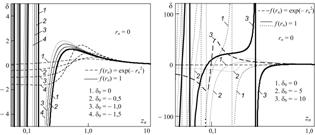
Рис. 4. Осевые распределения кривизны фронта волны в пучке с |
|
Распределения кривизны фронта волны вдоль оси фокусирующего излучателя с равномерным возбуждением приведены на рис. 4. В отличие от гауссового пучка, в зависимостях ![]() при
при ![]() в области дифракции Френеля (
в области дифракции Френеля (![]() ) присутствуют бесконечные разрывы (т.е.
) присутствуют бесконечные разрывы (т.е. ![]() ), координаты которых соответствуют четному числу фазовых зон на поверхности излучателя. Эта особенность связана с полной компенсацией вкладов фазовых зон и сопровождается появлением на оси пучка локального минимума с нулевой амплитудой. В местах прохождения зависимостью
), координаты которых соответствуют четному числу фазовых зон на поверхности излучателя. Эта особенность связана с полной компенсацией вкладов фазовых зон и сопровождается появлением на оси пучка локального минимума с нулевой амплитудой. В местах прохождения зависимостью ![]() нулевого значения форма участка фронта приосевой области пучка изменяется постепенно, в окрестности этих точек в волне формируется плоский участок фронта (
нулевого значения форма участка фронта приосевой области пучка изменяется постепенно, в окрестности этих точек в волне формируется плоский участок фронта (![]() ) и на оси пучка появляется максимум амплитуды. Это положение соответствует нечетному числу фазовых зон. С увеличением
) и на оси пучка появляется максимум амплитуды. Это положение соответствует нечетному числу фазовых зон. С увеличением ![]() трансформация фронта многократно повторяется, после чего на расстоянии
трансформация фронта многократно повторяется, после чего на расстоянии ![]() этот процесс вырождается в монотонное уменьшение кривизны до нуля и не зависит от распределения амплитуды на излучателе и величины
этот процесс вырождается в монотонное уменьшение кривизны до нуля и не зависит от распределения амплитуды на излучателе и величины ![]() .
.
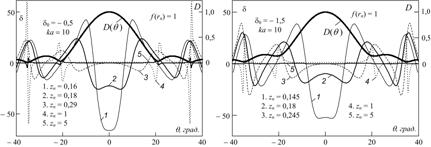
На рис. 5 приведены угловые распределения кривизны ![]() и характеристика направленности
и характеристика направленности ![]() фокусирующего излучателя при
фокусирующего излучателя при ![]() . Видно, что в узком интервале значений
. Видно, что в узком интервале значений ![]() форма волны претерпевает сильные изменения, которые сопровождаются трансформацией фронта с выпуклого на вогнутый и наоборот. С ростом
форма волны претерпевает сильные изменения, которые сопровождаются трансформацией фронта с выпуклого на вогнутый и наоборот. С ростом ![]() фиксируются положения локальных осцилляций в характеристике
фиксируются положения локальных осцилляций в характеристике ![]() , кривые 4 и 5, которые совпадают с границами лепестков
, кривые 4 и 5, которые совпадают с границами лепестков ![]() .
.
а )б)
Рис. 5. Угловые распределения кривизны и характеристика направленности ![]()
Список литературы:
1.Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. – М.: Наука, 1990. – 432 с.
2.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Наука, 1985. – 432 с.
3.Ахманов С.А., Никитин С.Ю.Физическая оптика. – М.: Наука, 2004. – 656 с
4.Гаврилов А.М.Фазозависимые процессы нелинейной акустики: модулированные волны. – Таганрог: Изд-во ТТИ ЮФУ, 2009. – 352 с.