Математические модели неопределённостей систем управления и методы, используемые для их исследования

Аннотация

Н.А. Целигоров, Е.Н. Целигорова, Г.В. Мафура

Описываются математические модели неопределённостей наиболее часто встречающихся в системах автоматического управления. Рассматриваются методы исследования систем автоматического управления при наличии неопределённостей, позволяющих достичь цели управления.

Ключевые слова: математические модели, неопределённости систем управления, методы исследования, робастная устойчивость, интервальные методы

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

05.13.18 - Математическое моделирование, численные методы и комплексы программ

В практике управления системами различного назначения (экономическими, финансовыми, техническими и др.) неизбежно приходится сталкиваться с различными затруднениями, вызванными так называемой неопределенностью. Неопределенность трактуется как неполнота или недостоверность информации об условиях реализации решения, наличия фактора случайности или противодействия.
Неопределенности могут быть вызваны экзогенными (определяемыми внешними воздействиями) или эндогенными факторами (определяемыми внутренними изменениями).
К эндогенным факторам можно отнести:

• параметрические;
• структурные;
• координатные;
• др. неопределенности.

Перечисленные неопределённости могут существенно ухудшить точность СУ и даже привести системы к потере работоспособности.
В теории управления выделено несколько основных типов неопределенностей.

1. Параметрическая неопределенность

В теории управления такая неопределенность является наиболее простым и хорошо изученным типом. Для него разработано большое количество методов синтеза законов управления, которые основаны на алгоритмах адаптивной настройки [1].
Модель «вход - выход» системы можно представить следующим соотношением:

.+.

,

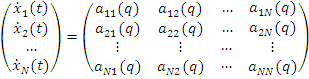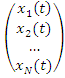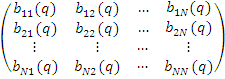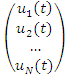или в векторном виде:

где вектор q – это вектор неопределенных параметров, , - матрицы неопределенных коэффициентов, независимых от времени. Такой тип неопределенности иногда называют структурированной неопределенностью.

2. Непараметрическая неопределенность

В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не полностью определенной передаточной матрице объекта неопределенность объекта может быть аддитивной, дробно-рациональной или мультипликативной. При этом уравнение выхода для модели с непараметрической неопределённостью будет выглядеть следующим образом [1]:

2.1. Аддитивная неопределенность

При аддитивной неопределенности модель «вход - выход» системы можно представить следующим соотношением:
+

.,

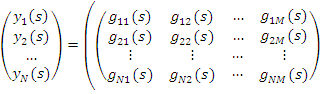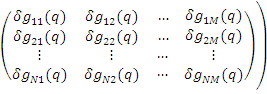
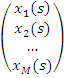или в матричном виде:

где y(s), x(s) – выходной и входной сигнал соответственно;
G(s) – передаточная матрица номинального устройства;
 - передаточная матрица не моделируемой динамики.

2.2. Дробно-рациональная неопределенность

При дробно-рациональной неопределенности модель «вход – выход» системы можно представить следующим соотношением:

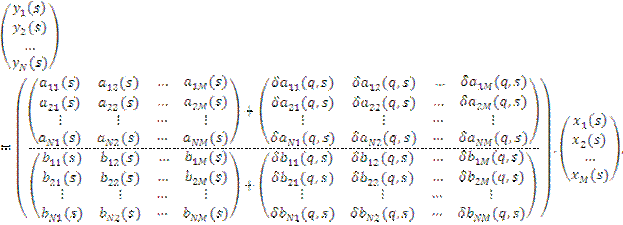
или для модели «вход – выход»

где y(s), x(s) – выходной и входной сигнал соответственно;
 - передаточная матрица номинального устройства;
 - числитель и знаменатель возмущения соответственно.

2.3. Мультипликативная неопределенность

При мультипликативной неопределенности [1] модель «вход – выход» системы можно представить следующим соотношением:

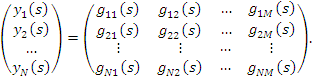
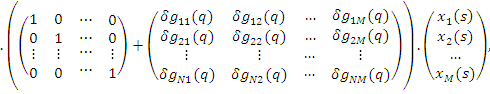
или для модели «вход – выход»

где y(s), x(s) – выходной и входной сигнал соответственно;
 - передаточная матрица номинального устройства;
 - передаточная матрица не моделируемой динамики.
E – единичная матрица соответствующей размерности.

3. Нестационарная неопределенность

Модель «вход – выход» для нестационарной системы управления можно представить в следующем виде [2]

.

+
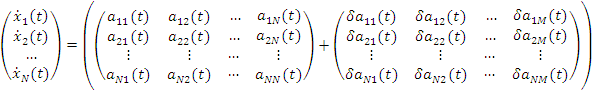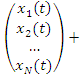
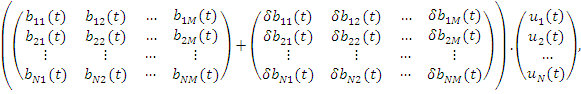
где коэффициенты матриц возмущения  и  ограничены некоторыми замкнутыми множествами и зависят от времени. Следует отметить, что связь между входом и выходом, этапы решения задач анализа и синтеза корректирующих устройств в отношении передаточных матриц в теории стационарных и нестационарных систем совпадают.

4. Нелинейнаянеопределенность

            В теории абсолютной устойчивости такая неопределенность описывается в виде характеристики нелинейного элемента (НЭ) принадлежащего сектору , удовлетворяет следующим равенствам [3]




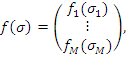
где  или , .

Любое звено системы может иметь нелинейную статическую характеристику. Нелинейности могут быть сопутствующими и корректирующими. К сопутствующим нелинейностям относятся нелинейности типа «люфт», «насыщение», «упор», которые оказывают, как правило, вредное влияние на поведение системы. Корректирующие нелинейности вводятся преднамеренно и предназначены для улучшения характеристик системы.

5. Неопределенность внешних условий

На поведение реальных систем управления значительное влияние оказывает окружающая среда, т.е. неконтролируемые внешние факторы, которые характеризуются высокой степенью неопределенности. Для ее преодоления используют различные методы идентификации или адаптивной компенсации возмущающих воздействий [4].

6. Неопределенность цели

При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т.п.) часто имеет место неопределенность цели, когда траектория движения, свойства среды функционирования, внешние воздействия и т. д. заранее неизвестны. В этом случае часто используются специальные методы нелинейного робастного управления [5].

Методы исследования систем автоматического управления при наличии неопределенностей

Методы исследования устойчивости систем автоматического управления при наличии неопределенностей условно можно также разделить на несколько типов:
1. Методы, основанные на достаточных условиях, в которых основным является понятие сверхустойчивости, формулируемое в терминах элементов матрицы, а не ее собственных значений. Причем, оно является достаточным условием асимптотической устойчивости. Это позволяет сводить задачу робастности к линейному или квадратичному программированию.
2. Вероятностные методы, в которых предполагается, что неопределенные параметры — случайные величины и о робастности системы судят с некоторой достаточно высокой вероятностью. Здесь удается решать задачи как с нелинейно входящей неопределенностью, так с большой размерностью систем.
3. Численные методы, использующие идеи теории возмущений, основываютсяна вычислении собственных значений возмущенной матрицы или корней полинома. Такие задачи робастного анализа и синтеза, как в полиномиальной, так и в матричной постановке позволяют осуществлять единообразный подход к их решению.
В условиях неопределенности первостепенную роль приобретают алгоритмы управления, позволяющие достигать цели управления, по возможности, за конечное время и обладающие свойством устойчивости по отношению к изменениям параметров и действию возмущений.
Большинство методов синтеза систем и алгоритмов управления основывается на некоторых основных принципах, к которым можно отнести:

• адаптивность;
• нейронные сети;
• системы с нечеткой логикой (fuzzy-контроллеры);
• системы с переменной структурой;
• синергетический подход;
• робастность;
• и др.

Методы адаптивного управления в условиях неопределенности являются одними из часто используемых путей решения задач управления сложными объектами. Адаптивными называются системы управления, которые в процессе эксплуатации при изменении параметров объектов или характеристик внешних воздействий самостоятельно, без участия человека изменяют параметры регулятора, его структуру, настройку или регулирующие воздействия для поддержания оптимального режима работы объекта [6].
Различают три класса адаптивных СУ:
1) самонастраивающиеся системы – в них могут автоматически изменяться параметры управляющих устройств;
2) самоорганизующиеся системы – в них может автоматически изменяться структура управляющих устройств;
3) самообучающиеся системы – это системы, в которых могут автоматически изменяться цели и критерии управления.
Синергетические методы анализа и синтеза управляемых нелинейных динамических систем, занимающие особое место в теории управления, направлены на повышение надежности и качества исследуемых объектов, функционирующих в условиях априорной неопределенности [7,8]. Их реализация предполагает решение следующих задач:

• разработку синергетических методов оценивания непосредственно неизмеряемых переменных нелинейных многосвязных систем;
• разработку синергетических методов оценивания неизмеряемых структурно неопределенных переменных нелинейных многосвязных систем;
• разработку синергетических методов синтеза управляемых нелинейных многосвязных систем;
• и ряда других.

Из перечисленных выше подходов особый интерес представляют алгоритмы робастного управления, которые к настоящему времени широко применяются в исследованиях различных САУ. Робастной называется система, обладающая устойчивостью (грубостью) свойств по отношению к изменениям параметров и действию возмущений [9]. Преимуществом такого подхода является то, что предоставляется возможность использовать интервальные методы [10], обладающие рядом особенностей, среди которых не требуется знание вероятностных характеристик неопределенностей, а также точного знания самих исходных параметров объекта управления, поскольку эти значения укладываются в определенный интервал.
Таким образом, выбор того или иного метода исследования СУ зависит от условий решения конкретной задачи управления, а также имеющиеся в наличие у исследователя программного обеспечения, реализующего тот или иной метод.

Литература

1. Цыпкин, Я.З. Частотные критерии робастной модальной линейных дискретных систем / Я.З. Цыпкин, Б.Т. Поляк // Автоматика.-1990. - № 5. - С.4-11.
2. Цыпкин, Я.З. Робастная устойчивость нелинейных дискретных систем при параметрической неопределенности / Я.З. Цыпкин // Автоматика.-1992.- № 4.- С.3-9.
3. Гелиг А.Х. Робастная устойчивость нелинейных импульсных систем / А.Х. Гелиг // Автоматика и Телемеханика. - 1996. - №12. -  С. 78-83.
4. Александров А.Г. Оптимальные и адаптивные системы / А.Г. Александров - М.: Высш. шк., 1989. – 384с.
5. Мирошник, И.В. Нелинейное и адаптивное управление сложными динамическими системами / И.В. Мирошник, В.О. Никифоров, А.Л. Фрадков  - СПб.: Наука, 2000.-549 с.
6. Ефимов Д.В. Робастное и адаптивное управление нелинейными колебаниями / Д.В. Ефимов — СПб.: Наука, 2005.— 314с.
7. Колесников А.А. Синергетические методы управления сложными системами. Теория системного синтеза / А.А. Колесников - М.: Едиториал УРСС: КомКнига, 2006. - 240 с.
8. Колесников, А. А. Синергетические методы управления сложными системами. Энергетические системы / А.А. Колесников, Г.Е. Веселов, А.Н.  Попов и др. - М.: Едиториал УРСС: КомКнига, 2006. - 248с.
9. Цыпкин Я.З. Робастно устойчивые нелинейные дискретные системы управления / Я.З. Цыпкин // Изв. РАН. Техн. кибернетика. -1992, № 6. - С.18-29.
10. Целигоров, Н.А. Алгебраические аспекты исследования робастной абсолютной устойчивости многомерных систем управления  / Н.А. Целигоров, Е.Н. Целигорова // Материалы Четвертой научной конференции «Системный синтез и прикладная синергетика». – Таганрог: Изд-во ТТИ ЮФУ, 2011. - С. 348-357.