Вложенные метаграфы как модели сложных объектов

Аннотация

С.В. Астанин, Н.В. Драгныш, Н.К. Жуковская

Вводится понятие вложенного метаграфа, как модели сложного объекта с различными уровнями обобщения. Показано, что вложенные метаграфы являются отражением общей системной концепции к описанию сложных объектов с синергетическим эффектом. Подобный подход позволяет перейти от теоретико-множественного описания сложных объектов к теоретико-алгебраическому описанию, что повышает адекватность модели реальным объектам. Рассматриваются некоторые приложения вложенных метаграфов, в частности в бизнес-анализе и организации семантического поиска.

Ключевые слова: вложенный метаграф, сложный объект, гиперребро как сущность, бизнес-анализ, семантическая сеть

05.13.01 - Системный анализ, управление и обработка информации (по отраслям)

05.13.18 - Математическое моделирование, численные методы и комплексы программ

В настоящее время используются различные подходы для представления знаний (продукционный, логический, семантический, фреймовый и т.д.), которые применяются в зависимости от специфики предметной области. Однако, для ряда сложно структурированных объектов, описание на основе перечисленных подходов, зачастую громоздко. В этой связи предлагаются новые подходы, в частности основанные на расширении теории графов и гиперграфов (метаграфы, эшграфы, и т.д.).
В работе вводится понятие вложенного метаграфа, как модели иерархического объекта с различными уровнями обобщения.
Метаграф S=(X, E) представляет собой графическое представление, состоящее из двух множеств X and E. Здесь X является порождающим множеством, а E – множеством ребер, определенных на порождающем множестве. Порождающее множество X метаграфа S есть множество элементов X={x₁, …, х_n} представляет собой переменные на концах ребер метаграфа [1].
Графическое представление метаграфа более ясно из следующего примера. Пусть S=(X, E) – метаграф, причем X={x₁, x₂, x₃, x₄, x₅, x₆, x₇} – порождающее множество и E={e₁, e₂, e₃, e₄} – множество ребер. Множество ребер может быть отображено так, как показано на рис.1, т.е. E={<{x₁, x₂}, {x₄}>, <{x₂, x₃}, {x₅}>, <{x₄, x₅}, {x₆, x₇}>, <{x₅}, {x₇}>}[2].

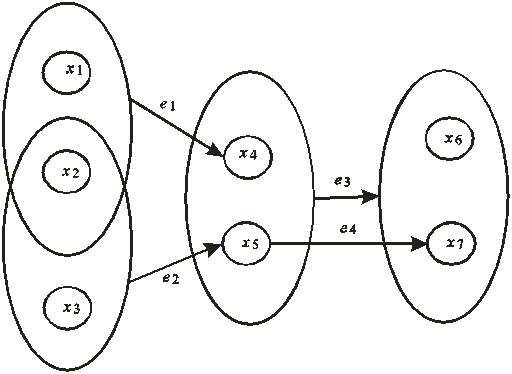
Рис.1.- Пример метаграфа

Как следует из примера, ребра отличаются друг от друга: одни связывают множество вершин с другим множеством (<{x₄, x₅}, {x₆, x₇}>) вершин или отдельной вершиной (<{x₁, x₂}, {x₄}>); вторые – определяют отношения между одиночными вершинами как в обычных графах (<{x₅}, {x₇}>). В теории гиперграфов отношение, связывающее совокупность вершин называется гиперребром, а в теории метаграфов – метавершиной. Таким образом, множество вершин метаграфа состоит из множества метавершин X_М, содержащих произвольное число элементов X и множества элементов X. В этом случае метаграф S можно задать следующим образом: S=(X, X_М, E, E_М), где X – порождающее множество; X_М – множество метавершин; E – множество ребер, определенных на множестве X; E_М – множество метаребер, определенных на множестве X_МX. В этом случае, используя предыдущий пример, представим метаграф S следующим образом: X={x₁, x₂, x₃, x₄, x₅, x₆, x₇}, X_М={x₈, x₉, x₁₀, x₁₁}, E={<x₅, x₇>}, E_М={<x₈, x₄>, <x₉, x₅>, <x₁₀, x₁₁>}, причем x₈={x₁, x₂}, x₉={x₂, x₃}, x₁₀={x₄, x₅}, x₁₁={x₆, x₇}.
На сегодня нельзя сказать, что сформирована теория метаграфов. Тем не менее, как следует из работ, в которых введено или используется понятие метаграфа, метаграф является конструкцией, совмещающей обычные графы и гиперграфы. Однако, гиперребро является отношением (свойством), определенным на множестве объектов, а любое отношение связывать с другим отношением или объектом этого отношения в любом языке – абсурдно, только если отношения не являются объектами рассмотрения. Например, отношения «любит-нравится» можно связать отношением «синоним». Однако, с математической точки зрения данные отношения, мы задаем как сущности: «любовь», «симпатия». Поэтому для метаграфов понятие гиперребра, как метавершины, должно иметь не смысл отношения, а смысл обобщения, как сущности, для элементов порождающего множества вершин. Например: X={я, ты, он, она}, X_М=({я, ты}, {он, она}, E={<она, я>}, E_М={<{я, ты}, {он, она}>}. Для определения введенных сущностей нам необходимо ввести отношения (ориентированные или неориентированные ребра) между элементами порождающего множества, т.е. расширить E, например следующим образом: E={<она, я>, <я, ты>, <ты, я>, <он, она>, {<она, он>}. Для данного частного примера, введенные понятия позволяют представить возможную структуру знаний известного четырехстишья: я-ты-он-она: вместе целая страна (рис.2). Использование гиперребра не только в качестве отношения, но и в качестве сущности, позволяет и более компактно описывать семантические сети сложных структур, за счет представления n-арных отношений «часть-целое (partof)», «есть, принадлежит (isa ...)» в виде сущностей. В данном случае, объекты, либо независимы, либо между ними введены синонимические отношения.

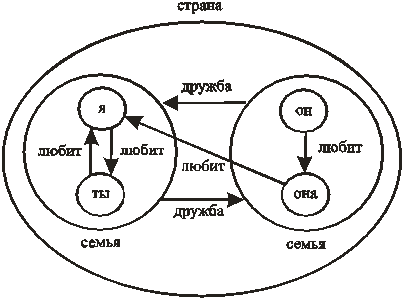
Рис.2.- Выделение метавершин как сущностей

Метаграф вложенности n (n-мерный граф) – это упорядоченная пара G=(X, E), где X={x_i}, – конечное непустое множество вершин, причем существуют функции f₁^l:g₁^l(x₁^l, e₁^l)x₂^p, f₂^p:g₂^p(x₂^p, e₂^p)x₃^r, …, f_n-1^t:g_n-1^t(x_n-1^t, e_n-1^t)x_n; E={e_k},  – множество ребер графа, где e_k=(V_i, W_i), , , т.е. каждое ребро n-мерного графа соединяет два подмножества множества вершин. Здесь i – определяет уровень вложенности, а индексы l, p, r, …, t – число вершин и ребер на соответствующем уровне.
Если ребро n-мерного графа является направленным, то граф называется ориентированным n-мерным графом. Вложенные метаграфы являются обобщением обычных графов, гиперграфов и метаграфов. В общем случае, вершины x₂^p являются гиперребрами графов g₁^l(x₁^l, e₁^l), вершины x₂^r являются гиперребрами графов g₂^p(x₂^p, e₂^p), и т.д. Ребра могут связывать вершины любого уровня представления, т.е. как отдельные вершины, так и гиперребра, что характерно для метаграфов. Подобное описание позволяет представлять вложенные структуры, каждая вершина которой может быть устроена по типу «револьверной матрешки» (рис.3).

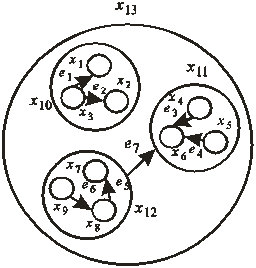
Рис.3.- Пример вложенного метаграфа трехмерной размерности

Вершина x₁ называется элементарной, если не существует g₀^s(x₀^s, e₀^s)x₁ при {x₀^s}= и {e₀^s}=.
Если все вершины вложенного метаграфа элементарные, то будем иметь обычный граф.
Если во вложенном метаграфе графе нет вершин с уровнем 3, т.е. для , то получим метаграф.
Если вложенный метаграф имеет уровень 2, т.е. все вершины второго уровня элементарные, а между ними нет ребер, то получим гиперграф.
Вложенные метаграфы являются отражением общей системной концепции к описанию сложных объектов с синергетическим эффектом. Действительно, каждый предмет, явление, процесс или ситуация, декомпозируемые на взаимосвязанные составные части, представляет собой сложный объект. Поскольку элементы сложного объекта взаимосвязаны, он, благодаря их взаимодействию, представляет собой нечто самостоятельное, однако существующее во взаимоотношениях с иными сложными объектами [3]. По определению система является совокупностью взаимосвязанных и взаимодействующих между собой элементов. Система находится в единстве со своим окружением и сама служит составным элементом систем высшего уровня. Ее же элементы выступают в качестве систем более низкого уровня. Представленное выше понятие вложенного метаграфа содержит и согласует между собой два важных свойства системы: единство(совокупность взаимосвязанных элементов) и делимость(каждый элемент системы - тоже система). Благодаря этому из системы можно выделить подсистемы. Это же позволяет в каждом конкретном случае сосредоточить внимание на системе или ее подсистеме, которая в данный момент наиболее интересует аналитика.
Рассмотрим некоторые приложения вложенных метаграфов.
Впервые понятие вложенного метаграфа было использовано при описании состояний нечеткой ситуационной сети [4], посредством которой моделировались неопределенные бизнес-процессы. Пусть S₁ = {S_н, S₂, …, S_p = S_ц} – совокупность состояний бизнес-процесса, причем S₁ – начальное состояние, а S_p – целевое состояние. Имея начальные и целевые описания состояний бизнес-процесса достаточно применить к начальным состояниям различные комбинации управляющих воздействий U, чтобы получить промежуточные состояния S₂, S₃, … . В свою очередь, воздействуя на промежуточные состояния можно получить новые состояния до тех пор, пока получим (или не получим) целевое состояние. В целом процесс перехода из одного состояния в другое удобно представить в виде ориентированного графа G = (S, V), где S = {S₁, S₂, …, S_p} – множество вложенных метаграфов, V = {V₁, V₂, …, V_l} – множество дуг (комбинаций управляющих воздействий) относительно верхнего уровня управления. На рис.4 представлен фрагмент такой сети, состояния которой являются метаграфами вложенности 3, а управляющие воздействия можно применить к любому уровню управления.

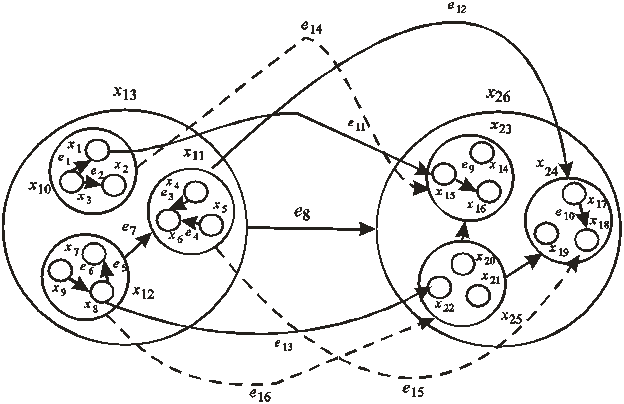
Рис.4.- Фрагмент ситуационной сети бизнес-процесса

Состояния сети x₁₃ и x₂₆ представлены метаграфами, причем состояние x₁₃ является обобщением ситуаций x₁₀, x₁₁ и x₁₂, а состояние x₂₆ – обобщением ситуаций x₂₃, x₂₄ и x₂₅. Каждое метаребро является управляющим воздействием, позволяющим перевести бизнес-процесс из одного состояния в другое состояние. При этом возможен анализ различных уровней в зависимости от текущих обстоятельств. Например, если в момент времени t ожидаемым состоянием является x₂₆, а фиксируется состояние x₁₃ при управляющих воздействиях e₁₁, e₁₂, e₁₃, то анализируются причины на других уровнях управления, не позволившие процессу перейти в состояние x26.
Другим приложением вложенных метаграфов является организация семантического поиска в глобальных и корпоративных сетях или электронных библиотеках. В частности, сегодня, при наличии огромного количества неструктурированных документов, наблюдается тенденция к формированию семантического Web.
Проблема семантического поиска, во многом будет решена за счет реализации подходов к структурированию документов. Одним из подходов является использование семантической аннотации отдельных структурных частей документа, что позволит с помощью набора семантических структур управлять глубиной поиска в документе. С этой целью будем предполагать, что документ структурирован подобно книжному изданию или научной статье. Вложенный метаграф, соответствующий структурированному документу, изображен на рисунке 3. Пусть гиперребро x₁₃ в целом представляет издание посредством описания названия, ФИО автора, аннотации и т.д. Гиперребра x₁₀-x₁₂ определяют разделы (главы) издания, причем содержание раздела x₁₂ используется в разделе x₁₁ (ребро e7). Каждый раздел состоит из трех подразделов. Например, раздел x₁₀ имеет подразделы x₁, x₂, x₃, причем контент подраздела x₃ используется в подразделах x₁, x₂.
Предположим, что существуют описания гиперребер и вершин вложенного метаграфа, в виде семантических сетей. Совокупность таких описаний назовем поисковым образом документа (ПОД). Формирование семантических сетей осуществляется любым известным способом аннотирования или реферирования текстов. Тогда можно предложить следующую процедуру информационного поиска в случае поискового образа запроса (ПОЗ), представленного совокупностью семантических сетей.
Ключевые слова запроса сравниваются с ключевыми словами гиперребра x₁₃, на основе методов поиска синтаксических ИПС. Если сравнение, по определенным критериям, успешно, то документ считается подходящим для анализа.
Семантические сети ПОЗ сопоставляются семантическим сетям разделов документа. Если сопоставление – успешно, то документ считается соответствующим запросу. Если сопоставление – неуспешно, то семантические сети сопоставляются семантическим сетям подразделов. Если какая-либо семантическая сеть ПОЗ, сопоставляется с какой-либо семантической сети подраздела, то документ считается соответствующим запросу.
Подобный подход позволяет выделить не только пертинентный документ, но и определить его часть, релевантную запросу пользователя.

Литература

1. R.Biswas, An Application of fuzzy sets in students evaluation [Text] // Fuzzy Sets and Systems, 1995.– Vol.74, №2.– pp.187–194.
2. D. Gaur, A. Shastri, R. Biswas and D. Seema Gaur Vague Metagraph [Text] //International Journal of Computer Theory and Engineering, 2009.– Vol.1, №2, June, – pp.1793–8201.
3. Глазунов Ю.Т.Графы и системы. Овеществление идеального [Текст] // Вестник Балтийского федерального университета им. И. Канта, 2011, Выпуск 10. –С.132-150.
4. Астанин С. В., Жуковская Н. К. Управление бизнес-процессами на основе их моделирования нечеткими ситуационными сетями [Электронный ресурс] //УБС, 2012. –№37. –С.145–163.