Приближенный расчет погонной индуктивности витой пары

Аннотация

А.В. Лабынцев, В.А. Лабынцев

Предложен достаточно простой алгоритм приближенного расчета погонной индуктивности витой пары, основанный на принципе средних геометрических расстояний ее поперечного сечения. Подтверждена работоспособность алгоритма и высокая точность получаемых результатов. Проведен сравнительный анализ взаимной погонной индуктивности длинной линии с взаимной погонной индуктивностью витой пары.

Ключевые слова: взаимная погонная индуктивность, длинная линия, витая пара

05.12.07 - Антенны, СВЧ устройства и их технологии

Вычисление многократного [1, формулы (3) и (4)] определенного интеграла, имеющего сложную параметрическую подынтегральную функцию, задача сложная. Она может быть решена только численно с помощью специальной программы. В то же время можно рассмотреть достаточно простой алгоритм приближенного расчета погонной индуктивности витой пары, в основе которого лежит принцип средних геометрических расстояний ее поперечного сечения.
Принцип средних геометрических расстояний применительно к расчету собственных индуктивностей формулируется следующим образом [2]: собственная индуктивность плоского контура из провода постоянного сечения при равномерном распределении тока по нему равна взаимной индуктивности соответствующих эквидистантных нитей, отстоящих одна от другой на расстояние, равное среднему геометрическому расстоянию площади поперечного сечения провода от самой себя.
Применение этого принципа к объемным контурам или к линиям с близко расположенными проводами все-таки приводит к ошибке. Но эта ошибка тем меньше, чем меньше радиус проводников контура по сравнению с расстоянием между их осями. Например, в случае прямой двухпроводной линии, сечение которой показано на рис.1, при a/R=2 погрешность такого расчета  составляет около 1,14%, а при a/R=4 уменьшается до 0.2%. Витые пары образуются, как правило, проводниками, расположенными вплотную друг к другу. Расстояние между осями проводов витой пары , где R – радиус провода, – толщина изоляции провода. Это обстоятельство выводит на первый план вопрос о точности результатов, получаемых с помощью рассматриваемого принципа применительно к витой паре.
Определим, для начала, выражение для коэффициента взаимной индукции двух произвольных параллельных нитей тока длинной линии. На рис. 1 изображено поперечное сечение двухпроводной линии со следами двух выделенных нитей тока di^‚ и di” .

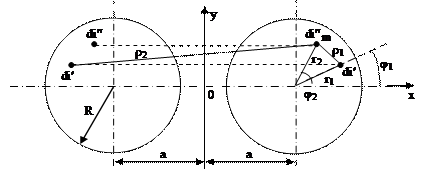
Рис. 1. - Поперечное сечение двухпроводной линии со следами двух выделенных нитей тока di^‚ и di”

Для такой модели векторный потенциал, создаваемый выделенными бесконечно протяженными нитями  тока di^‚ на правой ветви нити di” (в точке m), равен

,

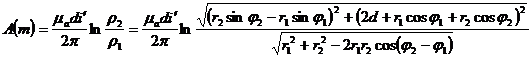а потокосцепление прямого и обратного участка нити тока di” длиной l  будет равно

.

Таким образом, погонная  взаимная индуктивность выделенных нитей тока равна

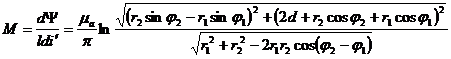,    (1)

а собственная погонная индуктивность такой линии определится интегралом –

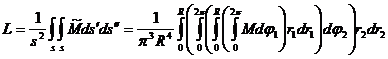.     (2)

Вычисление полученного интеграла доступно даже в среде MathCAD 2001. Результаты интегрирования для разных значений a/R приведены на графиках рис.2,а. Здесь же приводится зависимость погонной индуктивности Lc, рассчитанной по формуле (3-28) из справочника [2] (штриховая линия). Отдельным графиком (рис. 2,б) дается относительная разница этих результатов x

в процентах по отношения к справочным данным
.    (3)

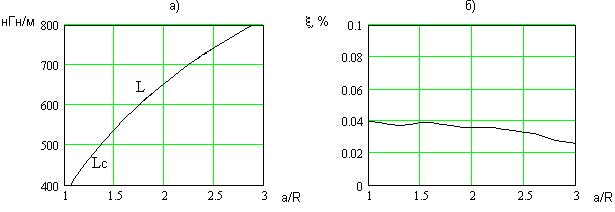
Рис. 2. - Результаты интегрирования для разных значений a/R

Графики, представленные на рис. 2, иллюстрируют практически полное совпадение результатов. Их разброс ξ обусловлен, по-видимому, только погрешностью численного интегрирования. Он не превышает 0.04%. Это значит, что взаимная индуктивность M для эквидистантных нитей, находящихся на среднем геометрическом расстоянии друг от друга, при малых a/R имеет некоторое, вполне определенное, расчетное значение, хотя и не выполняется утверждение принципа средних геометрических расстояний о том, что эта M=L.
Итак, справочное значение Lc для длинной линии имеет строго определенное значение (2) независимо от того, равно ли оно M, что имеет место при больших значениях a/R,  или не равно M, как при малых a/R. Но, как показано выше (рис. 2), между M и Lc существует строгое соответствие при любом a/R.
Сравним теперь взаимную погонную индуктивность M длинной линии с взаимной погонной индуктивностью Ms витой пары при весьма малых углах наклона жил пары. Для этого рассмотрим поперечное сечение длинной двухпроводной линии, как показано на рис. 3. Выделим две нити тока, находящиеся на расстоянии g друг от друга и параллельные осям проводников. Здесь
 - среднее геометрическое расстояние площади круга от самой себя.

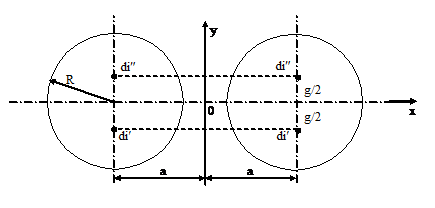
Рис. 3. - Поперечное сечение длинной двухпроводной линии

Рассчитаем взаимную погонную индуктивность M выделенных нитей для длинной линии по формуле (1). Одновременно вычислим взаимную погонную индуктивность Ms витой пары такого же поперечного сечения при малом угле наклона жилы b=2° в функции от a/R. Чтобы получить хорошую точность результатов, интегрирование проведем на протяжении двух шагов витой пары. Итак,
,
где
,

,



.

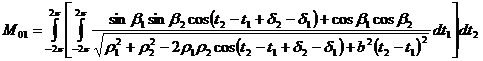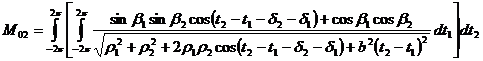
Результаты вычислений представлены в таблице 1. Их совпадение при b=2° достаточно хорошее: относительна погрешность определения Ms, по сравнению с M, не превышает 0.032% и уменьшается с ростом a/R.

Таблица № 1
Результаты вычислений взаимной погонной индуктивности

Следовательно, переходя к витой паре, т.е. к скручиванию длинной линии с углом наклона жилы b, можно с некоторым приближением погонную индуктивность пары Ls определить как
  (4)
где  - корректирующая функция. Значения этой функции для нитей тока, разнесенных на среднее геометрическое расстояние g=R×exp(-0.25),  рассчитаны в среде MathCAD, приведены в табл. 2  и иллюстрируются рис. 4.
Таблица № 2
Рассчитанные значения корректирующей функции

Пример. Рассчитаем погонную индуктивность витой пары из немагнитных материалов, у которой диаметр проводников равен 1 мм, толщина изоляции dИЗ=0.2 мм, а шаг скрутки h=17.5 мм. Исходными данными для расчета будут: отношение 

и угол наклона жилы
.
Погонная индуктивность такой пары будет равна

.

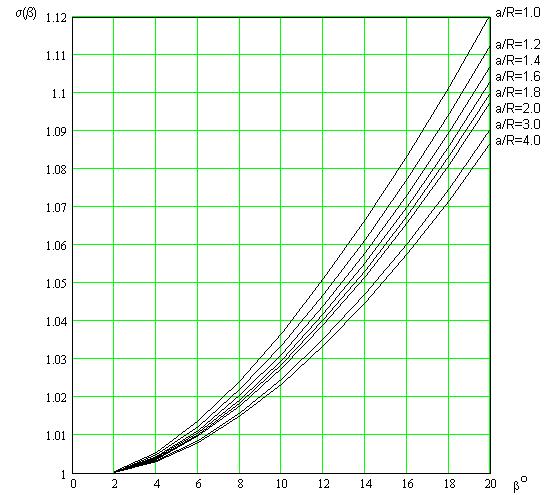
Рис. 4. - Результаты расчета в среде MathCAD

Результаты исследований изложенные в данной статье получены при финансовой поддержке Минобрнауки РФ в рамках реализации проекта "Создание высокотехнологичного производства по изготовлению информационно-телекоммуникационных комплексов спутниковой навигации ГЛОНАСС/GPS/Galileo" по постановлению правительства №218 от 09.04.2010 г.

Литература

1. Лабынцев А.В., Лабынцев В.А. Погонная индуктивность витой пары. [Текст] // Материалы Всероссийской научной конференции – Таганрог: Изд-во ТТИ ЮФУ, 2011. - С. 14-20.
2. Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. [Текст] // Справочная книга. – Л: «Энергия», 1970. – 416 с.