Исследование деформирования частично заглубленного фундамента при гармоническом воздействии с использованием метода граничных элементов и метода конечных элементов

Аннотация

М.И. Кадомцев, А.А. Ляпин, С.И. Тимофеев

Рассмотрен алгоритм совместного использования метода граничных элементов и метода конечных элементов при расчете заглубленного основания. Приведен пример расчета частично заглубленного фундамента, лежащего на трехслойной полуплоскости. Проанализированы распределения перемещений под фундаментом в зависимости от частоты воздействия и сочетания физических параметров упругих полос и упругого полупространства.
Ключевые слова: динамика, вибрация, гармонические колебания, МГЭ, МКЭ.

05.23.17 - Строительная механика

Проблемы повышения долговечности зданий и сооружений в качестве составляющей включают разработку и реализацию методов их расчета при учете всех возможных факторов воздействия, которые могут привести к развитию и накоплению разрушений. Одним из недостаточно изученных в этом плане являются воздействия на объекты колебаний и волн, распространяющихся в грунтовом массиве от источников различной природы (от сейсмических, до техногенных). В строгой постановке решение этой проблемы связано с необходимостью совместного расчета здания или сооружения с грунтовым массивом. Эта задача требует не только больших вычислительных ресурсов, но и развития методов, описывающих процесс распространения колебаний в слоистых полуограниченных массивах, содержащих нарушения структуры и локализованные неоднородности.
В настоящее время при расчете  зданий и сооружений на возможное сейсмическое (или техногенное) воздействие используются упрощенные способы задания воздействия на объект колебаний, распространяющихся в грунте. Это связано с тем фактом, что расчет конкретных сооружений производится на основе программных комплексов, в основу которых чаще всего заложен метод конечных элементов (МКЭ). Моделирование процессов возбуждения и распространения колебаний и волн в геофизической среде в основном связан с геофизическими приложениями и использует аналитические и аналитико-численные методы [1,2]. Это объясняется тем, что грунтовый массив представляет полуограниченную область (наиболее распространенная модель геофизической среды – многослойное полупространство), а использование метода конечных элементов при решении подобных модельных задач связано с необходимостью ее аппроксимации конечными телами, что может вызвать большую погрешность расчета, особенно на низких частотах колебаний, характерных для сейсмического диапазона.
Существенно, что система «Геологическая среда – массивный поверхностный объект», как правило, обладает резонансными свойствами. Причем наиболее выраженным является первый, низкочастотный (до 5 Гц) резонанс  [3]. Сейсмическое воздействие на удалении от эпицентра связано с распространением поверхностной волны, имеющей также низкочастотный спектр и, соответственно, большую длину волны. Последние факты определяют необходимость разработки подходов, позволяющих более точно учитывать реальные условия и резонансный характер динамического взаимодействия геологической среды и поверхностного массивного объекта при набегании волн, распространяющихся в грунтовом массиве от источника сейсмических или техногенных колебаний. Этот подход, в качестве элемента, должен предусматривать сочетание математических методов моделирования колебаний геофизической среды (аналитических или аналитико-численных методов) с методами расчета напряженно-деформированного состояния элементов конкретного сооружения (на основе МКЭ).
Основная сложность определена корректным МКЭ моделированием грунтового массива. Здесь можно использовать два подхода. Первый  определен выбором достаточно большого по размерам «представительского» объема. Размеры области берутся с таким расчетом, чтобы продольная волна, отраженная от фиктивной границы представительского объема грунтового массива, в течение времени наблюдения не достигала объекта. Недостатком этого метода, при простоте реализации, является быстрое увеличение количества степеней свободы при увеличении времени наблюдения, которое достигает числа, превышающего возможности вычислительной техники.
Второй подход состоит в том, что «представительский» объем грунта окружается специальными «буферными» слоями. Все физические характеристики «буферных» слоев полностью совпадают с параметрами грунта, за исключением вязкости, которая плавно возрастает к границам грунтового массива. За счет повышения вязкости удается вполне достоверно смоделировать затухание упругих волн на бесконечности.        Техническим недостатком этого подхода является то, что для каждой новой структуры грунта и типа воздействия приходится выполнять достаточно большой объем работ по определению размеров представительского объема, толщины «буферных» слоев и коэффициентов диссипации. Во-вторых, для многих задач количество степеней свободы остается слишком велико для решения на ПЭВМ.
В данной работе предлагается расчет с использованием алгоритма, являющимся дальнейшим развитием  методик моделирование системы «здание – грунт» с использованием метода конечных элементов. приведены примеры расчета воздействия осциллирующей сосредоточенной нагрузки на фундамент, устроенный на слоистом грунтовом основании с использованием описанного гибридного  метода МКЭ-МГИУ [3], приводятся примеры расчета воздействия осциллирующей сосредоточенной нагрузки на фундамент, устроенный на слоистом грунтовом основании с использованием описанного гибридного  метода МКЭ-МГИУ.
1. Постановка задачи
Рассматриваемая область представляет собой с (рис. 1)
Перемещение точек среды удовлетворяют уравнениям Ламе
     (1)
где  - оператор Лапласа.
При рассмотрении  задачи будем считать, что заданы  условия жесткой стыковки слоев слоистого полупространства, фундамента и здания между собой, что соответствует требованию непрерывности перемещений и напряжений при переходе через границу раздела сред. Следует отметить, что область приложения нагрузки и тип фундамента не влияют на дальнейшие рассуждения. Также, для большей ясности изложения, задачу будем рассматривать в плоской постановке, что никоим образом не ограничивает общности метода. 

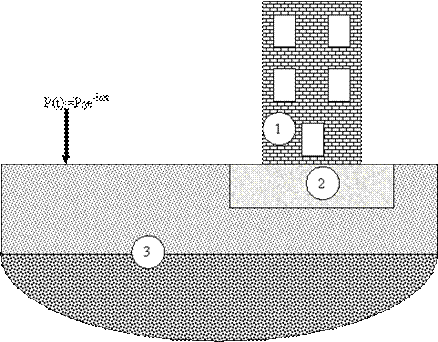
Рис. 1
Исследуемая область. Цифрами обозначены: 1 – здание, 2 – фундамент, 3 – грунтовый массив.

Для решения поставленной задачи предлагается следующая последовательность действий
1) Рассматриваемая область разбивается на две части по некоторой фиктивной границе g (рис.1). Выбор границы разделения в общем случае произволен. Например, это может быть граница здания и грунта.
2) Каждая из двух частей области разбивается на сетку конечных элементов. Обязательным является условие совпадения узлов сеток граничных и конечных элементов на фиктивной границе g (рис.3).

Рис. 2
Соответствие узлов конечноэлементной сетки на границе g

3. Для дальнейших рассуждений воспользуемся линейностью поставленной задачи. Пусть граница g разбита на N узлов сетки конечных элементов. Тогда на границе g имеем N неизвестных усилий R_k, k=1..N (рис.4). Представим усилия R_k в виде (2)
    (2)
Здесь  и  проекции соответственно на оси OX и OY,  и  - единичные силы, сонаправленные с ортами осей ОХ  и OY соответственно.
Учитывая (2), перемещения на границе можно представить в виде (3)

      (3)

Здесь  - перемещения в j-м узле от единичного усилия, приложенного в k-м узле в направлении орта i_l,  - неизвестные интенсивности усилий.

1. Аналогичным образом, построив решение для верхней части получим

    (4)

Далее приведены примеры расчета воздействия осциллирующей сосредоточенной нагрузки на фундамент, устроенный на слоистом грунтовом основании с использованием описанного гибридного  метода МКЭ-МГИУ.
Следует отметить, что, с одной стороны, данная задача представляет практический интерес сама по себе – например, при моделировании воздействия от бура, гидромолота или вибратора для погружения обсадных труб при обустройстве вибронабивных свай на фундаменты зданий. В перечисленных случаях, как показывают неоднократные эксперименты, возможно представление воздействия как сосредоточенной, осциллирующей силы.
С другой стороны, другие, наиболее распространенные источники техногенного воздействия – проезд автомобильного транспорта, железнодорожного транспорта, забивка свай, производство взрывных работ, также могут быть успешно смоделированы с использованием решения задачи в данной постановке. В этих случаях отклик на нестационарное воздействие можно представить как суперпозицию решений стационарных задач с привлечением методов гармонического анализа.
Наиболее актуально решение исследуемой задачи при строительстве зданий и сооружений в условиях плотной городской застройки. В последние годы, несмотря на некоторое снижение объемов строительства вследствие финансового кризиса, количество возводимых в черте города зданий остается очень высоким. В таких условиях является очень актуальной возможность смоделировать влияние техногенных воздействий при производстве строительных работ на фундаменты близлежащих зданий с учетом реальных грунтовых условий. В настоящий момент методики, позволяющие адекватно смоделировать динамическое воздействие и учесть его при проектировании, практически отсутствуют.
Исследуемая область (рис. 1) представляет собой фундамент, лежащий на слоистом грунтовом основании. Грунтовое основание рассматривается как пакет из двух полос, лежащих на однородной полуплоскости. Фундамент моделируется прямоугольником, частично заглубленным в верхний слой.
Физические свойства среды описываются плотностью  и скоростями распространения поперечных и продольных волн: .
Условия стыковки разнородных сред считаются жесткими с требованием непрерывности векторов перемещений и напряжений при переходе через границы раздела.
На поверхности среды вне фундамента задана сосредоточенная сила, осциллирующая с частотой .
При моделировании фундамента с помощью метода конечных элементов использовались прямоугольные четырехузловые плоские конечные элементы.
Граница стыковки методов МКЭ и МГИУ совпадает с границей раздела фундамента и верхнего слоя грунтового основания.
Модель среды  линейно-упругая, перемещения точек среды удовлетворяют уравнениям Ламе.
При расчете по вышеописанной модели были исследованы три случая, которые в соответствии с существующими теоретическими и экспериментальными исследованиями представляются наиболее характерными.
А) Случай однородного полупространства. Как однородное пространство могут быть с хорошей степенью приближения смоделированы грунты, в которых либо верхний слой разреза грунтового массива имеет настолько большую толщину, что вкладом отраженной от нижележащих слоев волны можно пренебречь, либо механические характеристики верхних слоев разреза мало отличаются друг от друга.
Б) Случай структуры, в дальнейшем обозначаемой как «мягкий-жесткий-мягкий» («мжм»). В этом случае, между верхним слоем и полупространством, имеющих близкие механические характеристики, находится «жесткий» слой, скорость распространения волн в котором существенно выше.
В) Случай структуры, в дальнейшем обозначаемой как «жесткий-мягкий-жесткий» («жмж»). В этом случае, между верхним слоем и полупространством, имеющих близкие механические характеристики, находится «мягкий» слой, скорость распространения волн в котором существенно ниже.
Физические свойства слоев, используемые для каждого из случаев, приведены в таблице 2. Следует подчеркнуть, что для большей наглядности результатов механические характеристики верхней полосы остаются неизменными при всех вариантах расчета. Ширина полос для всех случаев также постоянна и составляла 6м для первой от дневной поверхности полосы, и 3 м для второй.
Графики вертикальных перемещений, полученные по результатам расчета, приведены на рис. 3-6. Расчет проводился в диапазоне частот 2-100Гц. Следует отметить, что многослойная полуплоскость со структурой «жесткий-мягкий-жесткий» является резонансной с частотой резонанса f=18Гц, а структура «мягкий-жесткий -мягкий» имеет резонанс на частоте f=50Гц.
На рисунках графики, соответствующие однородному полупространствам и структурам «жесткий-мягкий-жесткий» и «мягкий-жесткий -мягкий»  обозначены как «opp», «zmz» и  «mzm» соответственно.
По результатам исследования можно сделать выводы, что

1. С ростом частоты амплитуда перемещений падает.
2. На всех частотах, кроме частоты f=50 Гц, амплитуда перемещений наибольшая для структуры «жесткий-мягкий-жесткий»
3. На частоте f=50 Гц, являющейся резонансной для структуры «мягкий-жесткий-мягкий» для этой структуры амплитуда перемещений в сравнении с другими рассмотренными структурами максимальна.

Таблица 2 – физические характеристики сред, использованные при расчетах

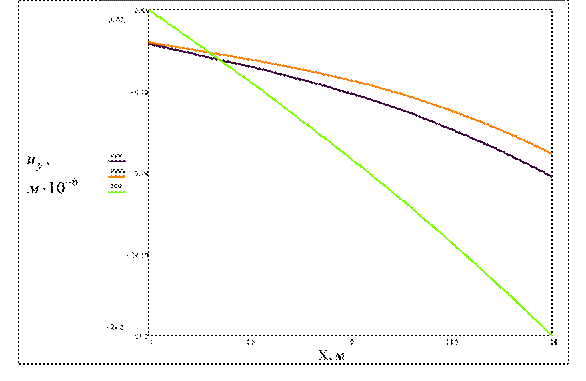
Рис. 3
Распределение перемещений uy под бетонным фундаментом. Частота воздействия f=2 Гц

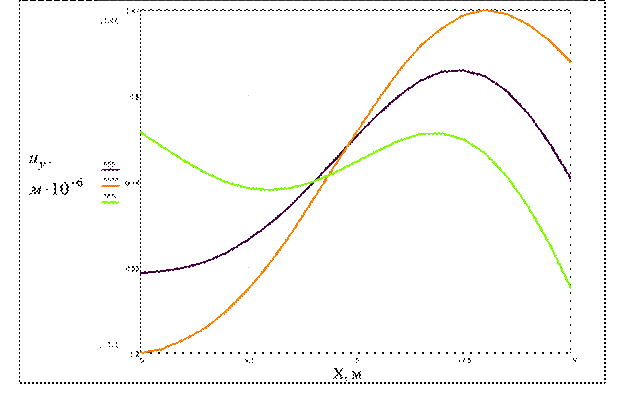
Рис. 4
Распределение перемещений u_y  под бетонным фундаментом. Частота воздействия f=18 Гц

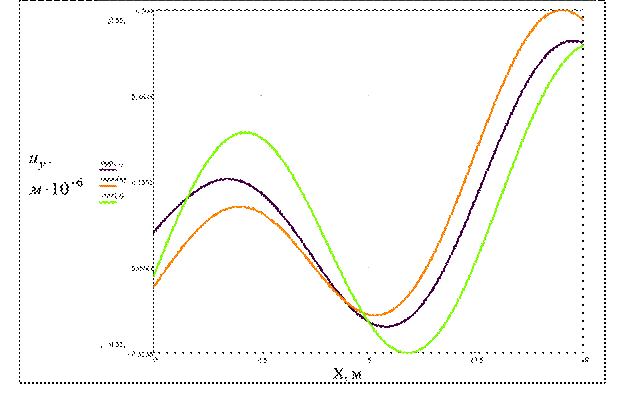
Рис. 5
Распределение перемещений u_y  под бетонным фундаментом. Частота воздействия f=50 Гц

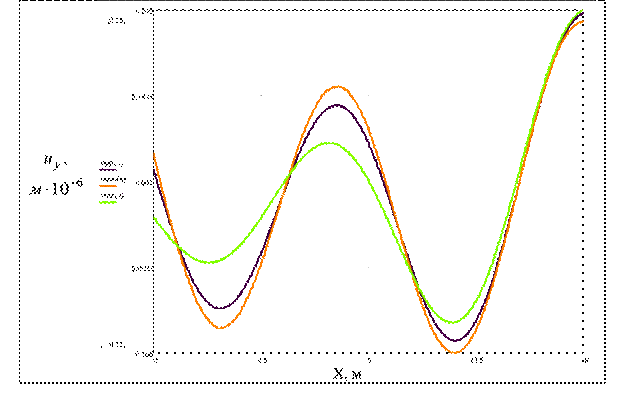
Рис.6
Распределение перемещений uy под бетонным фундаментом. Частота воздействия f=100 Гц

По результатам исследования можно сделать выводы, что

1. С ростом частоты амплитуда перемещений и напряжений падает.
2. На всех частотах, кроме частоты f=50 Гц, амплитуда напряжений и перемещений наибольшая для структуры «жесткий-мягкий-жесткий»
3. На частоте f=50 Гц, являющейся резонансной для структуры «мягкий-жесткий-мягкий» для этой структуры амплитуда перемещений и напряжений в сравнении с другими рассмотренными структурами максимальна.

Литература

1.Бабешко, В.А.Динамика неоднородных линейно-упругих сред / Бабешко, В.А., Глушков, Е.В., Зинченко, Ж.З.. – М. : Наука; Главная редакция физико-математической литературы. 1989. – 343 с.
2.Ляпин, А.А.  Механико-математические модели в задачах активной сейсмологии / Ляпин, А.А., Селезнев, М.Г., Собисевич, Л.Е., Собисевич, А.Л.– М. : ГНИЦ ПГК(МФ) при КубГУ Минобразования России, 1999. – 249 с.
3.Кадомцев, М.И.Исследование динамики заглубленных фундаментов методами граничных и конечных элементов / Кадомцев, М.И., Ляпин, А.А., Селезнев, М.Г. //  Строительная механика и расчет сооружений. – 2010. – № 3. – С.61–64.