Некоторые аспекты обратимости процессов в линейных электрических цепях второго порядка
Аннотация
Дата поступления статьи: 23.11.2013В работе приводится определение обратимости, которое может быть использовано в теории линейных электрических цепей. Для определения условий протекания процессов в обратной последовательности выбрана линейная электрическая цепь второго порядка, содержащая два реактивных элемента L и C. Для линейной электрической цепи в момент коммутации ток (или напряжение) можно представить в виде суммы двух составляющих: принужденной и свободной. Условия обратимости для принужденной составляющей тока (или напряжения) можно добиться соответствующим изменением параметров независимых источников электрической энергии. Для свободной составляющей обратимость процесса можно обеспечить, изменив знаки элементов цепи таким образом, чтобы знаки корней характеристического уравнения изменились на противоположные.
Ключевые слова: Обратимый процесс, электрическая цепь, ток, коммутация, многополюсник, входное сопротивление, характеристическое уравнение
05.13.05 - Элементы и устройства вычислительной техники и систем управления
В настоящее время, как в научной, так и в учебной литературе можно встретить различное толкование свойства обратимости. Так, например, в теории линейных электрических цепей свойство обратимости формулируется в виде теоремы обратимости (взаимности) [1].
Другое толкование свойства обратимости заключается в том, что процесс x(t) считается обратимым, если, начиная с некоторого момента времени 
, процессы в исследуемой системе проходят в обратной последовательности [2] (рис. 1). В данной работе используется второе понимание свойства обратимости процессов.
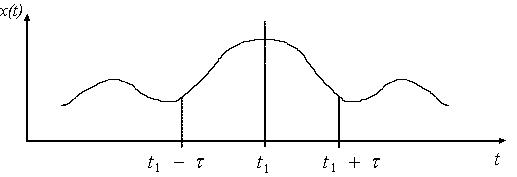
Рис. 1. – Свойство обратимости процесса x(t)
Определение. Процесс изменения силы тока 
(или напряжения 
) в одной из ветвей электрической цепи будем называть обратимым в том случае, когда, начиная с некоторого момента времени 
, в результате изменения параметров схемы замещения электрической цепи (коммутации), выполняется условие:
. (1)
Или
.
В основе многих форм движения материи лежат электромагнитные взаимодействия. Поэтому условия протекания обратимого процесса, полученные при изучении обратимости в электрических цепях, могут быть распространены и на другие формы движения материи, механическую, тепловую и т.п. Эти результаты в перспективе могут быть применены при решении проблем в различных областях практической деятельности (энергетика, экология, медицина, гидромеханика и т.п.) [3, 4, 5, 6, 7]. Так, например, создав условия обратимости в электронной модели при исследовании аварийных ситуаций в электрических цепях, можно выявить последовательность нарушения режимов работы отдельных устройств. В этой связи тема данной работы представляется актуальной.
Целью данного исследования является определение изменений в линейной электрической цепи второго порядка (коммутаций), при выполнении которых ток будет изменяться, начиная с некоторого момента времени 
в обратной последовательности. Рассмотрим схему замещения произвольной линейной электрической цепи второго порядка (рис. 2).
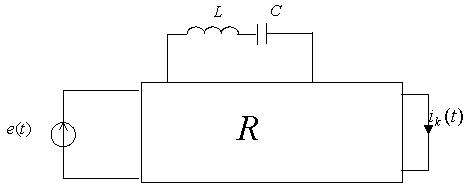
Рис. 2. – Схема замещения произвольной линейной электрической цепи второго порядка
Здесь 
- источник напряжения; R – линейный резистивный пассивный многополюсник; L – индуктивность; С- ёмкость; 
- ток в 
- й ветви.
Пусть требуется в этой электрической цепи произвести в заданный момент времени 
коммутацию таким образом, что бы ток (или напряжение) в ветви 
стал изменяться в обратной последовательности. В общем случае для заданного класса электрических цепей ток 
изменяется по закону:
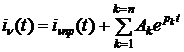, (2)
где 
- принуждённая составляющая тока; 
- постоянные интегрирования; 
- корни характеристического уравнения; 
- порядок электрической цепи.
Применяя к (2) условие (1) для схемы после коммутации, получим:
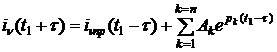. (3)
Путём несложных преобразований уравнение (3) можно привести к виду:
.
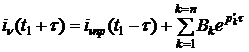где 
; 
.
Требуемого закона изменения принуждённой составляющей можно добиться, изменив соответствующим образом параметры независимых источников электрической энергии в цепи. Обратимость процесса для свободной составляющей можно обеспечить, изменив знаки соответствующих элементов таким образом, что бы знаки корней характеристического уравнения изменились на противоположные.
В качестве примера рассмотрим условия обратимости для свободной составляющей тока 
в схеме замещения линейной электрической цепи второго порядка (рис. 2).
Известно [8], что для схемы замещения на рис. 2 свободная составляющая тока 
для моментов времени 
может быть представлена в виде:
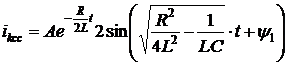. (4)
Если для моментов времени 
к уравнению (4) применить условие (1), то получим:
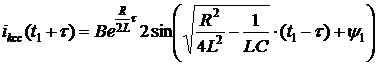. (5)
В выражениях (4) и (5) R - эквивалентное входное сопротивление резистивного многополюсника со стороны LC – контура. Таким образом, для того, чтобы вещественная часть корня поменяла знак на противоположный, достаточно поменять знак входного сопротивления. Можно показать, что для этого достаточно поменять знаки активных сопротивлений, входящих в состав резистивного многополюсника. Данная коммутация может быть реализована, если все резисторы в составе многополюсника синтезировать на основе аналого-цифро-аналоговых элементов [9, 10].
Работа выполнена при поддержке гранта №213.01-24/2013-96 «Разработка и исследование распределенной системы интеллектуального управления процессом производства, передачи и распределения энергии»;
Работа выполнена при поддержке гранта Президента Российской Федерации МД-1098.2013.10;
Работа выполнена при поддержке гранта НШ-1557.2012.10.
Литература:
1. Сешу С., Балабанян Н. Анализ линейных цепей [Текст]: Монография / С. Сешу, Н. Балабанян. – Москва: Изд-во «Госэнергоиздат», 1963. – 551с.
2. Савельев И.В. Курс физики. Том 1. Механика. Молекулярная физика [Текст]:Монография/И.В. Савельев. – Москва: Изд-во «Наука», 1989. – 350 с.
3. Фиговский, О. Нанотехнологии: сегодня и завтра (зарубежный опыт, обзор) [Электронный ресурс] // «Инженерный вестник Дона», 2011, №3. – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2011/511 (доступ свободный) – Загл. с экрана. – Яз. рус.
4. Дробашева Т.И., Расторопов С.Б. Термостойкость кислородных щелочных вольфрамовых и молибденовых бронз [Электронный ресурс] // «Инженерный вестник Дона», 2013, №1. – Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1488 (доступ свободный) – Загл. с экрана. – Яз. рус.
5. Набережных А.И., Деменев А.В. Теория и практика создания энергоэффективной бытовой холодильной техники, работающей при экстремально высокой температуре окружающей среды [Электронный ресурс] // «Инженерный вестник Дона», 2013, №2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1620 (доступ свободный) – Загл. с экрана. – Яз. рус.
6. Karamov F.A. Investigations of Reversible and Polarised Interfacial Surface Properties by Electrochemical Impedance Method // Materials Science Forum.Trans Tech Publications, Switzerland, 1998. – Vols. 289 – 292. – P.871-878. – Режим доступа: // http://www.scientific.net/MSF.289-292.871 (доступ: 28$) – Загл. с экрана. – Яз. англ.
7. Daniel R. Cornejo, F.P. Missell. Study of Reversible and Irreversible Magnetization Processes Using the Moving Preisach Model // Materials Science Forum.Trans Tech Publications, Switzerland, 1999. – Vols. 302 – 303. – P.53-58. – Режим доступа: // http://www.scientific.net/MSF.302-303.53 (доступ: 28$) – Загл. с экрана. – Яз. англ.
8. Нейман Л. Р., Демирчян К.С. Теоретические основы электротехники. Том1 [Текст]: Монография / Л. Р. Нейман, К.С. Демирчян. – Ленинград: Изд-во «Энергоиздат», 1981. – 530 с.
9. Басан С.Н., Изотов М.В. Применение микропроцессорных устройств в задачах синтеза нелинейных электрических цепей с заданными свойствами [Текст] // Материалы VII Международной научно-практической конференции «Перспективные исследования науки и техники – 2011». Технические науки, Промышленность, наука и образование, 2011. – № 56. – С.17-24.
10. Басан С.Н., Изотов М.В. К проблеме выбора аналого-цифрового элементного базиса при реализации нелинейных резистивных двухполюсников с заданными вольтамперными характеристиками [Текст] // Известия вузов. Электромеханика. 2010. – №6. – С.80-83.