Разработка модели взаимодействия лазерного излучения с биологическими тканями

Аннотация

И.В. Куликова, С.П. Малюков, С.И. Петерс

Дата поступления статьи: 25.10.2013

В статье представлена математическая модель теплового воздействия лазерного излучения на биологические структуры. В модели учтена анизотропия оптических и тепловых параметров биологических структур, учтены процессы охлаждения поверхности за счет конвекции и излучения. Разработано программное обеспечение на основе численных методов и полученной модели. Приводятся результаты моделирования воздействия двух типов лазеров эрбиевого (λ = 2,94 мкм) и СO2 (λ = 10,6 мкм) на биологическую структуру, состоящую из эмали и дентина.

Ключевые слова: лазерные биотехнологии, численное моделирование, температурное поле

05.13.18 - Математическое моделирование, численные методы и комплексы программ

Современные медицинские технологии основаны на фундаментальных исследованиях в области физики, математики, биологии и химии. Одно из направлений исследований это применение лазерных технологий в медицине, которое открывает новые возможности не только в эстетической медицине, но и при лечении серьезных заболеваний. Взаимодействие лазерного излучения с биотканями в медицинских исследованиях и терапии основано на использовании широкого разнообразия эффектов взаимодействия света с биологическими тканями. Все процессы взаимодействия лазерного излучения с биологическими объектами в зависимости от плотности мощности и времени воздействия делят на три группы [1-4]:

• лазерная диагностика, не оказывает заметного влияния на объект воздействия;
• лазерная терапия, оказывает специфическое или неспецифическое воздействие на биообъекты;
• лазерная хирургия и деструкция биотканей.

Кроме того биологические объекты можно разделить по оптическим характеристикам на сильно рассеивающие среды, которые являются оптически мутными – это кожа, мышечная ткань, мозг, кровь и т.д. и на слабо рассеивающие, прозрачные среды – это роговица и хрусталик глаза [1-4].
Лазерная терапия и лазерная хирургия связаны с неспецифическим тепловым воздействием на биологические объекты. Распределение температуры определяет степень воздействия на обрабатываемые ткани и уровень теплового удара на окружающие ткани, который стремятся свести к минимуму. Важнейшими параметрами лазера, определяющего режим обработки и степень теплового воздействия, являются: режим облучения (непрерывный или импульсный), время и распределение плотности мощность по сечению лазерного луча, а так же длина волны, которая определяет интенсивность поглощения излучения биотканью. Параметры биотканей, определяющие режим обработки и степень теплового воздействия, являются: теплопроводность, теплоемкость и плотность ткани, поглощательная способность (коэффициент экстинкции) и коэффициент рассеивания, а так же многослойность и сложность любой биологической структуры.
Разработка тепловой модели лазерного взаимодействия с биологическими структурами
Распределение температуры в биологической структуре является одним из основных параметров в лазерных медицинских технологиях. Работа посвящена разработке тепловой модели взаимодействия лазерного излучения с биологическими тканями. Тепловое моделирование процесса обработки биологической структуры позволит оптимизировать нагрев окружающих тканей и тем самым повысить качество лазерной биотехнологии.
Поглощенная энергия лазерного излучения вызывает в облученном участке биологической структуры локальное повышение температуры. При этом часть тепла отводится из зоны обработки за счет кондукции вглубь лежащие биоткани, вызывая зачастую нежелательный нагрев, часть тепла с обрабатываемой поверхности за счет конвекции и излучения отводится в окружающее пространство. Стоит заметить, что в теплоотводе необходимо учитывать излучательную составляющую, поскольку уже при температуре в 60 оС она начинает превалировать над конвективной составляющей [2, 5-7].
Распределение температуры в твердом теле описывается уравнением теплопроводности, которое для анизотропного случая будет иметь вид [5]:
,      (1)                                       
где с – удельная теплопроводность;  - плотность; Т – температура в структуре; t – время;  - оператор Набла; - коэффициент теплопроводности; q – плотность мощности источника тепла.
Излучательный и конвекционный процессы отвода тепла с обрабатываемой поверхности будут описываться следующими выражениями [5];
,    (2)                                        
,  (3)                                            
где  – коэффициент излучения,  – постоянная Стефана-Больцмана, h – конвективный коэффициент, ,  – плотность теплового потока за счет излучения и конвекции соответственно,  – температура окружающей среды.
Суммарный тепловой поток  с поверхности будет описываться выражением:
,   (4)                                        
где  – суммарный коэффициент теплопередачи.
Источником тепла является лазерное излучение, которое частично отражается от обрабатываемей поверхности, поглощается материалом и проникает в него. Затухание лазерного луча за счет поглощения и рассеивания его энергии биологическим телом, которое является оптически мутной средой, происходит по экспоненциальному закону и описывается законом Бугера - Ламберта - Бера для серых тел [5,6]:
,   (5)                                      
где  – плотность мощности лазерного луча с учетом затухания;  – плотность мощность лазерного луча; R – коэффициент отражения;  – коэффициент экстинкции, состоящий из поглощательной способности среды –  и коэффициента рассеивания –  [6]; y – координата направленная вглубь материала от обрабатываемой поверхности.
В уравнении (1) не учтено поглощение тепла за счет фазовых переходов (испарения), а так же перенос тепла за счет тока крови, поскольку во многих случаях данные эффекты не вносят существенного вклада в теплообмен [2,6]. В качестве граничных условий для поверхности был взят суммарный тепловой поток, описываемый выражением (4), для вглубь лежащих тканей была задана температура тела, т.е. использовались граничные условия первого рода.
Нестационарное уравнение теплопроводности (1) для двумерного случая будет иметь следующий вид:
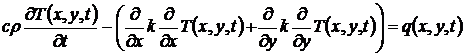,   (6)          
с граничными условиями третьего рода (4) для поверхности   с учетом уравнения Фурье [2] будут иметь вид:
,   (7)                                    
граничными условиями первого рода для внутренних областей , которые имеют вид:
,  (8)                                            
и начальными условиями, описываемыми следующим выражением:
, (9)                                          
Уравнение (6) с соответствующими начальными (9) и граничными условиями (7), (8) не решается аналитически. Для его решения был использован метод конечных разностей [8, 9, 10] на неравномерной прямоугольной сетке, который позволил учесть так же анизотропию биологических тканей. Поскольку толщина слоев в биологических структурах может меняться от нескольких десятков микрон до десятков сантиметров, то шаг сетки определялся толщиной каждого слоя. Так же при выборе шага сетки учитывался размер сечения лазерного луча.
В конечно-разностном виде для неравномерной сетки  система уравнений (6)-(9) будет иметь следующий вид:
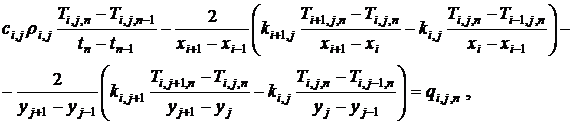(10)
для внутренних точек области , , ,
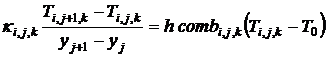,  (11)                      
где , при , , ;
, (12)                                              
при , , ; при , , ; при , , ,
       (13)                                          
при , , .
Внутренний источник тепла равен поглощенному теплу и будет описываться следующим выражение [6]:
,  (14)                               
где  – мощность лазерного луча в соответствующих точках координат и во времени, которая в конечно-разностном виде будет иметь вид:
 (15)                                    
Выражения (10) – (15) представляют собой систему нелинейных алгебраических уравнений. Нелинейность вносит излучательная составляющая. Для решения данной системы был использован итерационный алгоритм, который был реализован в системе Matlab.
Результаты моделирования
В качестве тестовой биологической структуры был использован зуб, состоящий из эмали толщиной 20 мкм и дентина, при воздействии эрбиевым (l = 2,94 мкм) и СO₂ (l = 10,6 мкм) лазерами. Тепловые и оптические параметры дентина и эмали зуба существенно отличаются от характеристик мягких биотканей для данных длин волн и приведены в таблице 1 [1, 3, 4]. Результаты моделирования распределения температуры приведены на рис. 1.

Таблица № 1
Оптические и тепловые параметры дентина и эмали

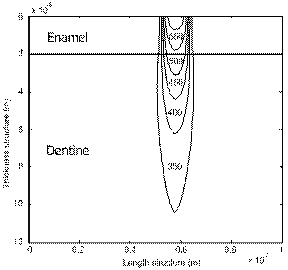
Результаты моделирования хорошо согласуются с экспериментальными данными, приведенными в литературе [1, 3, 4], и показывают, что длинна волны лазера существенно влияет на режим обработки биотканей. Так для СO₂ лазера глубина теплового проникновения в 1,5 раза больше, чем для эрбиевого лазера [1, 3, 4], что хорошо согласуется с результатами моделирования, приведенными на рис. 1.

а)	б)

Рис. 1 – Распределение температуры в структуре эмаль дентин при обработке лазером с длинной волны а) l = 2,94 мкм и б) l = 10,6 мкм

Заключение

Разработанная модель и программное обеспечение учитывает следующие особенности взаимодействия лазерного излучения и биотканями:

• сложную многослойную структуру биотканей;
• отражение лазерного излучения о поверхности;
• затухание лазерного луча в структуре;
• конвективную и излучательную составляющие при охлаждении поверхности биологической структуры;
• зависимость оптических и тепловых свойств от типа тканей входящих в структуру.

Данная модель положена в основу программного обеспечения, для проведения численных экспериментов, которые позволяют более детально исследовать влияние различных параметров лазера (плотность мощности, время воздействии, режим, длина волны), самой обрабатываемой ткани (коэффициент теплопроводности, удельная теплоемкость, плотность, коэффициентов рассеивания и экстинкции) и показать степень влияния длины волны лазерного излучения на результаты воздействия, что позволит минимизировать тепловой удар на окружающие биоткани и, как следствие, существенно уменьшить биологическую деградация структуры.
Результаты исследований, изложенные в данной статье, получены при финансовой поддержке Минобрнауки РФ в рамках реализации ФНИР
№ 4.6131.2011 "Исследование отображения состояния человека в пространстве признаков и разработка методов обеспечения информационно-психологической устойчивости человека при неблагоприятных информационных воздействиях"

Литература:

1. Тучин В.В. Лазеры и волоконные световоды в биомедицинских исследованиях. [Текст] //  – М.: Изд-во ФИЗМАТЛИТ, 2010. – 500 с.
2. Малюков С.П., Куликова И.В., Бростилов С.А. Моделирование теплового воздействия лазерного излучения на биологические ткани. [Текст] // Фундаментальные исследования. Часть 2. – 2012. ‑№ 11. – C. 425-429.
3. John D.B. Featherstone, Peter Rechmann, Daniel Fried. IR laser ablation of dental enamel [Text] // SPIE. 2000. Vol. 3910, pp. 136–148.
4. Fried D., Shori R., Duhn C. Backspallation due to ablative recoil generated during Q−switched Er: YAG ablation of dental hard tissue [Text] // SPIE. 1998. Vol. 3248, pp. 78–84.
5. Самарский А. А., Вабищевич П. Н. Вычислительная теплопередача. [Текст] // – М. : Едиториал УРСС, 2003. ‑ 784 с.
6. Малюков С.П., Куликова И.В., Калашников Г.В. Моделирование процесса лазерного отжига структуры «кремний-стекловидный диэлектрик» [Текст] // Известия ЮФУ. Технические науки. Тематический выпуск «Интеллектуальные САПР». – 2011. – № 7. – С. 182-188.
7. Рындин Е.А., Исаева А.С., Рыжук Р.В. Математическая модель механических напряжений, инициированных лазерным импульсом [Текст] // Фундаментальные исследования. – 2012. – №11. – С.609 – 614
8. Рындин Е.А., Леньшин А.С. Методика численного моделирования спектрометрических газочувствительных сенсорных систем. [Текст] // «Инженерный вестник Дона», 2012, № 4, Ч. 2. – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1360 (доступ свободный) – Загл. с экрана. – Яз. Рус.
9. Проценко Е.А. Двумерная конечно-разностная модель формирования наносов в прибрежной зоне водоема и ее программная реализация [Текст] // «Инженерный вестник Дона», 2010, № 3, – Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2010/224 (доступ свободный) – Загл. с экрана. – Яз. Рус.
10. Онишкова А.М. Численное решение задачи для плоской области со свободной границей. [Текст] // «Инженерный вестник Дона», 2012, № 4, ч. 1 – Режим доступа: http://www.ivdon.ru/magazine/archive/n4p1y2012/1205 (доступ свободный) – Загл. с экрана. – Яз. Рус.