Эффекты размытия фазовых переходов в сегнетоэлектриах-релаксорах
Аннотация
Дата поступления статьи: 30.10.2013В сегнетоэлектриках сложного состава со структурой перовскита не наблюдается четкого фазового перехода. В этой сегнетоэлектриков наблюдается релаксационный характер диэлектрической поляризации в области фазового перехода.
Ключевые слова: Фазовые переходы, сегнетоэлектрики, перовскиты, сложные оксиды, сегнетоэлектрики-релаксоры
Одна из актуальнейших проблем современной физики в области исследования фазовых переходов связанна с исследованием сегнетоэлектриков сложного состава со структурой типа перовскита, в которых не наблюдается четкого фазового перехода. В связи с этим появилось новое название сегнетоэлектрик с размытым фазовым переходом. В таких сегнетоэлектриках наблюдается релаксационный характер диэлектрической поляризации в области фазового перехода. Такие опытные факты удается объяснить, если предположить, что размытие фазового перехода обусловлено флуктуациями состава. Согласно этим представлениям различные области кристалла (линейный размер ~100 А) имеют различные температуры Кюри. Предполагается, что релаксация обусловлена 1) движением границ между полярной и неполярной фазами или 2) зарождением и исчезновением полярных областей. Второй механизм был рассчитан в работе, в которой была обобщена теория Дебая на случаи, когда число релаксаторов меняется с температурой (с максимумом: в средней точке Кюри Тср). При таком подходе возникает возможность объяснения различных опытных фактов, например температурной зависимости ε [1, 2, 3].
Для эффектов релаксационной поляризации микроскопических полярных областей в сегнетоэлектриках–релаксорах [4, 10] при ![]() описывается законом (1)
описывается законом (1)
![]() , (1)
, (1)
где ![]() – константы; m – принимает значение от 1,5 до 2,0 [5,7]. Также отличительным признаком сегнетоэлектриков–релаксаров является существование спонтанной поляризации сопутствующих ей свойств (пьезоэффекта, пироэффекта и др.) при
– константы; m – принимает значение от 1,5 до 2,0 [5,7]. Также отличительным признаком сегнетоэлектриков–релаксаров является существование спонтанной поляризации сопутствующих ей свойств (пьезоэффекта, пироэффекта и др.) при ![]() . Отметим, что
. Отметим, что ![]() в этих объектах увеличивается с увеличением частоты измерительного поля.
в этих объектах увеличивается с увеличением частоты измерительного поля.
Таблица. Температурно-зависимые коэффициенты по петлям гистерезиса в представлении полиномами
Коэффициенты |
Материалы |
||
|
PMN |
0.9PMN-0.1PT |
PLZT 12/40/60 |
|
|
A0(Vm/C) |
1,04·108 |
0,17·108 |
5,55·108 |
|
A1(Vm/CK) |
-0,79·106 |
-0,21·106 |
-2,67·106 |
|
A2(Vm/CK2) |
1,57·103 |
0,53·103 |
3,25·103 |
|
B0(Vm5/C3) |
-3,23·109 |
0,29·109 |
8,65·109 |
|
B1(Vm5/C3K) |
2,11·107 |
-0,15·107 |
-8,73·107 |
|
B2(Vm5/C3K2) |
-3,46·104 |
0,16·104 |
16,6·104 |
|
C1(Vm9/C5) |
1,04·1010 |
1,6·109 |
-4,19·1011 |
|
C1(Vm9/C5K) |
-5,17·107 |
0 |
2,90·108 |
|
C2(Vm9/C5K2) |
8,07·104 |
0 |
-4,51·106 |
|
Коэффициенты |
Материалы |
||
|
PLZT 9/65/35 |
SBN |
BTS-3.5 |
|
|
A0(Vm/C) |
1,24·108 |
0,14·108 |
1,89·108 |
|
A1(Vm/CK) |
-0,62·106 |
-0,12·106 |
-1,27·106 |
|
A2(Vm/CK2) |
0,84·103 |
0,26·105 |
2,14·103 |
|
B0(Vm5/C3) |
1,38·109 |
-1,97·109 |
4,08·109 |
|
B1(Vm5/C3K) |
-1,31·107 |
0,63·107 |
-2,18·107 |
|
B2(Vm5/C3K2) |
2,3·104 |
0 |
12,8·104 |
|
C1(Vm9/C5) |
1,24·1011 |
4,11·1010 |
-2,17·1013 |
|
C1(Vm9/C5K) |
-7,19·108 |
-1,18·108 |
1,57·1013 |
|
C2(Vm9/C5K2) |
1,08·106 |
0 |
-2,83·108 |
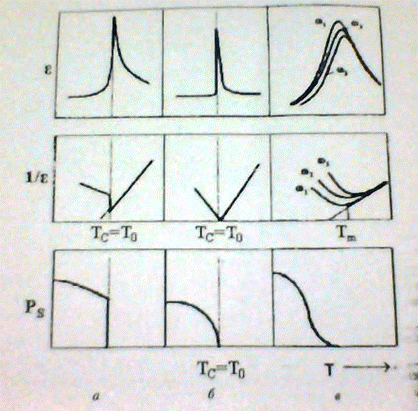
Рис.2. Гистограмма локальных ![]() для различных количеств дислокации в объеме
для различных количеств дислокации в объеме ![]() : сплошные линии – аппроксимации распределения функции Гауса; a – 1; б – 10; в – 50; г – 100
: сплошные линии – аппроксимации распределения функции Гауса; a – 1; б – 10; в – 50; г – 100
В работе [6, 8, 9] подробно анализируется модель, в которой выдвигаются следующие положения:
– в релаксорах существуют микроскопические полярные области, обусловленные неоднородностью распределения атомов разного сорта;
– эти области независимы, т.е. каждая область имеет свой дипольный момент, который может независимо переключиться;
– в ромбоэдрической фазе дипольные моменты могут ориентироваться только в одном из направлений [111].
С использованием термодинамической теории Ландау плотность свободной энергии для сегнетоэлектриков-релаксаров можно записать как (2):
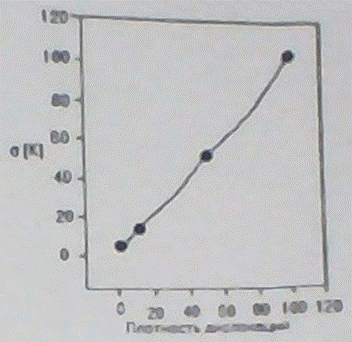
Рис.3. Зависимость полуширины гауссовской функции ![]() и числом дислокаций
и числом дислокаций
![]() (2)
(2)
Температурно-зависимые коэффициенты A(T), B(T), C(T) могут быть определены по петле гистерезиса в их представлении полиномами (3)
![]() ;
; ![]() ; (3)
; (3)
![]()
В таблице приведены результаты таких расчетов при обработке экспериментальных данных для материалов PMN, 0.9PMN-0.1PbTiO3, PLZT 12/40/60, PLZT 9/65/35, SBN и BTS – 3.5.
Во всех рассмотренных материалах в релаксорных фазах величина дипольных моментов уменьшается с увеличением температуры. При увеличении температуры до Tm монодоменный кристалл разбивается на малые полярные области. Этот процесс продолжается до предельной температуры ![]() . При более высоких
. При более высоких ![]() концентрация полярных областей уменьшается, и кристалл становится нормальным параэлектриком.
концентрация полярных областей уменьшается, и кристалл становится нормальным параэлектриком.
Литература:
1. Смоленский Г.А. Научная сессия Отделения общей физики и астрономии академии наук СССР совместно с Отделением физико-технических и математических наук Академии наук Молдавской ССР – Кишинев, 1973 г., С.331-351.
2. Ляпин А.А., Кадомцев М.И., Тимофеев С.И. Исследование деформирования частично заглубленного фундамента при гармоническом воздействии с использованием МКЭ– // «Инженерный вестник Дона», 2011, №4. –Режим доступа: http://www.ivdon.ru/magazine/ archive/n4y2011 /700 (доступ свободный) – Загл. с экрана. – Яз. Рус.
3. Снежков В.И. , Столбовская Н.Н. , Камошенкова Е.В. , Корабельников Г.Я. Направления повышения конкурентоспособности коммерческих банков на рынке автокредитования в Ростовском регионе– // «Инженерный вестник Дона», 2012, №4 (часть 2). –Режим доступа: http://ivdon.ru/magazine/ archive/n4p2y2012/1315 (доступ свободный) – Загл. с экрана. – Яз. Рус.
4. Cross L.E. // Ferroelectrics. 1987. V.76. P.241-267
5. Смоленский Г.А., Боков В.А., Исупов В.А. и др. Сегнетоэлектрики и антисегнетоэлектрики // Л. 1971. С.476.
6. Skulski R. The diffusion of the phase transitions in the selected groupsof ferroelectrics and relaxors. Katowice, 1999, P.345
7. Skulski R. // Mater. Sci. and Engineering. 1999. V.B64. P.39-43.
8. Захарченко И.Н., Дудек Ю., Дудкевич В.П. и др. // Рукопись деп. ВИНИТИ. 1985. № 2956 – В88. с.423.
9. Surowiak Z., Margolin A.M., Birukov S.V. et al/ // Inzynieria materialova. 1988. V.4. P. 87-95.
10. Блинц P., Жекш Б. Мягкие моды в сегнетоэлектриках и антисегнетоэлекриках. М, 1975, с.398