Оценка справедливой цены опциона для обобщенной модели КоксаРоссаРубинштейна в случае состояний

М.Н. Богачева; Л.И. Прянишникова

Оценка справедливой цены опциона для обобщенной модели Кокса-Росса-Рубинштейна в случае m-состояний

Аннотация

М.Н. Богачева, Л.И. Прянишникова

Дата поступления статьи: 04.12.2013

Рассматривается оценка справедливой цены опциона для обобщенной модели Кокса-Росса-Рубинштейна в случае m-состояний. Формулируются утверждения. На основании выводов, полученных в работе построено программное приложение, позволяющее произвести расчеты.

Ключевые слова: модель Кокса-Росса-Рубинштейна, справедливая цена опциона, рисковый актив, процентная ставка

05.13.18 - Математическое моделирование, численные методы и комплексы программ

В качестве модели эволюции цен основных ценных бумаг на финансовом рынке рассмотрим систему двух дискретных стохастических уравнений, описывающих безрисковый и рисковый активы [1, 2].
Пусть и эволюционируют согласно формулам:

где и - постоянная процентная ставка;

где и - последовательность m-значных случайных величин:

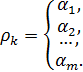
Значения случайной величины проанализируем следующим образом:

пусть ;
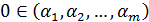обозначим

((1)

Будем считать, что каждый из атомов при переходе от этого шага к дробится ровно на частей.
Таким образом, в соответствии с обозначениями (1), имеем

Введем функцию (см. [3, стр. 46])
,
где и – параметры рассматриваемой обобщенной модели Кокса-Росса-Рубинштейна, см. формулу (1). При этом находим из уравнения

Рассмотрим европейский опцион на покупку с платежным обязательством
.
В этом случае
.
Пусть

Ясно, что при функция и, следовательно, . Пусть . Тогда имеем:

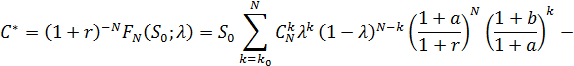
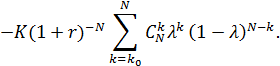
Полагая

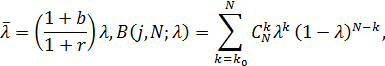
получаем следующее следствие формулы Кокса-Росса-Рубинштейна [3, c.50].
Теорема. Для европейского опциона на покупку с платежным обязательством рассматриваемого в рамках модели (1), справедливая цена опциона определяется формулой

где , причем .

Нахождение цены аналогично рассмотренному выше.

Теорема. Для европейского опциона на покупку с платежным обязательством рассматриваемого в рамках модели (1), справедливая цена опциона определяется формулой

где , причем ;
, .

Рассмотрим оценку параметров обобщенной модели Кокса-Росса-Рубинштейна [4, 5, 6]. Качественная оценка параметров модели позволит использовать результаты, полученные выше для дальнейшего исследования. Обычно рассматривают три вида оценки параметров: на основе метода максимального правдоподобия, на основе ранговых статистик, и на основе знаковых статистик. Однако, первые два метода требуют знание закона распределения. Поэтому в работе применена непараметрическая схема оценки параметров, которая была ориентирована на знаковые статистики [7].
Расчет параметров нашей модели произведем на основе статистической информации. Происходит статистическая обработка данных стоимости акций и курсов валют (доллар и евро) за 2010 год. Данные получены с сайта rbc.ru. Выборка содержит более 6 тыс. записей. Нами проанализированы следующие виды акций: Американский доллар, Аэрофлот, ДальЭнерго, Евро, ЕЭС России, ИркутскЭнерго, Лукойл, МосЭнерго, РБК, Ростелеком, Ростовэнерго, Самараэнерго, Саратовэнерго, Свердловэнерго, СибНефть, Сургутнефтегаз, Уралсвязь, УралСиб, ЮКОС.
Данные хранятся в базе данных Акции.dbf (файл инсталлируется вместе с программой).
В качестве параметров модели нами выбраны:

a - минимальная процентная ставка,
b - максимальная процентная ставка,
c - минимальное падение процентной ставки,
d - минимальный рост процентной ставки
r - среднее значение процентной ставки.

Вышеуказанные параметры модели анализируются для двух любых выбранных активов за период с 1.01.2010 по 31.12.2010.
При выборе активов из списка важно, какой из активов выбирается первым, а какой вторым. Первый выбранный актив играет роль рискового актива, второй же безрискового[8]. При этом появляется возможность "перекачки" средств из одного актива в другой [9].
По результатам, полученным в статье, построено программное приложение, позволяющее произвести расчет справедливой верхней цены опциона и расчет нижней цены опциона [10]. Таким образом, получен интервал цен, придерживаясь которого можно минимизировать риск при работе на финансовом рынке, модель которого совпадает с обобщенной моделью Кокса-Росса-Рубинштейна.
Программное приложение позволяет:

выбрать тип ввода параметров модели: статистический или пользователем;
выбрать два вида актива при статистическом поиске параметров модели: в первом столбце пользователь выбирает рисковый актив, во втором списке безрисковый актив;
ввести данные для расчета: необходимо задать начальную цену акции; количество времен; контрактную цену.
получить справедливую цену опциона для верхнего и нижнего хеджа (рис. 1).

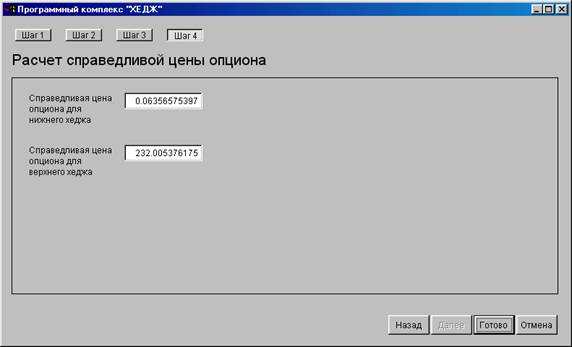
Рис. 1. – Программный комплекс для расчета справедливой цены опциона.

Таким образом, были изучены основные методы оценки параметров модели (1), и в качестве оптимального выбран метод знаковых статистик.

Литература:

1. Cox J.C., Ross R.A., Rubinstein M. Option pricing a simplified approach [Text] //Journal of Financial Economics. 1976. – Vol. 7 (september). – Р.229-263.
2. Harrison J.M., Pliska S.R. Martingales and stochastic integrals in the theory of continuous trading [Text] // Stochastic Process. Appl. 1981. – Vol. 11, №3. –Р.215-260.
3. Мельников, А.В. Финансовые рынки: стохастический анализ и расчет производных ценных бумаг [Текст] / А.В. Мельников. – Москва: ТВП, 1997. – 126 с. – ISBN 5-85484-023-5.
4. Красий, Н.П. О безарбитражности и полноте обобщённой модели финансового рынка в случае скупки акций [Текст] / Н.П. Красий, И.В. Павлов // Обозрение прикладной и промышленной математики – Москва, ТВП. 1999. – Т.6. №1. – С.162-163.
5. Мисюра, В.В. Расчёт хеджирующих стратегий для опционов европейского типа в случае (B,S)-рынка относительно специальной хааровской фильтрации [Текст] // Сборник научных трудов III Всероссийского симпозиума "Математическое моделирование и компьютерные технологии". Кисловодск, 1999. – Т.4. – С.62-64.
6. Красий Н.П. О вычислении спрэда для обобщённой модели (B,S)-рынка в случае скупки акций [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru/magazine/archive/n4p2y2012/1378 (доступ свободный) – Загл. с экрана. – Яз. рус.
7. Болдин М.В., Симонова Г.И., Тюрин Ю.Н. Знаковый статистический анализ линейных моделей [Текст] / М.: ФИЗМАТЛИТ, 1997. – 288 с. – (Теория вероятностей и математическая статистика.) – ISBN 5-02-015222-6.
8. Белявский, Г.И., Мисюра В.В., Павлов И.В. Исследование модели (В,S)-рынка относительно специальной хааровской фильтрации [Текст] / Г.И. Белявский, В.В. Мисюра, И.В. Павлов // Международная школа-семинар по геометрии и анализу памяти Н.В. Ефимова. Тезисы докладов. Ростов-на-Дону, 1998 – С. 179-181.
9. Белявский, Г.И. Ранговый критерий полноты одного финансового рынка при допущении арбитража [Текст] / Г.И. Белявский, В.В. Мисюра, И.В. Павлов // Обозрение прикладной и промышленной математики. – Москва, ТВП. 1999. – Т.6. №1. – С.164-165.
10. Шишкова А.Н. Программный комплекс τ-полнота (B, S)-рынка в случае специальной хааровской фильтрации при допущении арбитража [Электронный ресурс] // «Инженерный вестник Дона», 2012, №4 (часть 2). – Режим доступа: http://ivdon.ru/magazine/archive/n4p1y2012/1174 (доступ свободный) – Загл. с экрана. – Яз. рус.