Расчёт на прочность армированных балок с заполнителем из бимодульного материала с использованием различных теорий прочности
Аннотация
Дата поступления статьи: 04.12.2013В работе рассматривается произвольно опёртая, произвольно нагруженная армированная балка с заполнителем из бимодульного материала. Выведены формулы для определения касательных напряжений, возникающих в заполнителе с учётом действия армированных элементов. Получены формулы для главных напряжений, возникающих в произвольной точке заполнителя, а также уравнения для определения точки, в которой главные напряжения достигают экстремальных значений. Приведены условия прочности по классическим теориям прочности, а также по критериям прочности , применяемым для расчёта конструкций из бимодульного материала.
Ключевые слова: армированная балка,бимодуль упругости,нормальное напряжения,теории прочности.
Рассматривается произвольно опёртая, произвольно нагруженная балка, армированная стержнями параллельно оси балки. Заполнитель изготовлен из бимодульного материала, т.е. модули упругости на растяжение и сжатие различны, но материал является изотропным. Доказано [1], что для таких материалов верны гипотезы и формулы сопротивления материалов и теории упругости.
В [2] были получены формулы нормальных напряжений, возникающих в заполнителе:
![]() =
= ![]() =
= ![]() , (1)
, (1)
![]() =
= ![]() =
= ![]() , (2)
, (2)
Где z – расстояние от нейтральной линии 0y до точки, в которой определяется нормальное напряжение,
![]() - изгибающий момент относительно нейтральной линии в произвольном поперечном сечении балки,
- изгибающий момент относительно нейтральной линии в произвольном поперечном сечении балки,
n – число стержней арматуры,
![]() - осевой момент инерции поперечного сечения одного стержня арматуры,
- осевой момент инерции поперечного сечения одного стержня арматуры,
![]() - изгибающий момент, возникающий в одном стержне арматуры,
- изгибающий момент, возникающий в одном стержне арматуры,
![]() - модуль упругости при растяжении стержней арматуры,
- модуль упругости при растяжении стержней арматуры,
![]() - изгибающий момент, возникающий в бетонной части балки,
- изгибающий момент, возникающий в бетонной части балки,
![]() - изгибающий момент, возникающий в растягивающей части бетона,
- изгибающий момент, возникающий в растягивающей части бетона,
![]() - модуль упругости бетона (заполнителя) при растяжении,
- модуль упругости бетона (заполнителя) при растяжении,
![]() - осевой момент инерции растягивающей части бетона,
- осевой момент инерции растягивающей части бетона,
![]() - изгибающий момент, возникающий в сжимающей части бетона,
- изгибающий момент, возникающий в сжимающей части бетона,
![]() - модуль упругости бетона (заполнителя) при сжатии,
- модуль упругости бетона (заполнителя) при сжатии,
![]() - осевой момент инерции сжимающей части бетона.
- осевой момент инерции сжимающей части бетона.
Используя (1), (2) найдём выражение касательных напряжений, возникающих в растянутой и сжатой зоне заполнителя:
![]() , (3)
, (3)
где ![]() поперечная сила в сечении, в котором определяется
поперечная сила в сечении, в котором определяется ![]() –
–![]()
![]() растянутой и сжатой зоны.
растянутой и сжатой зоны.
Главные напряжения, возникающие в произвольной точке заполнителя в растянутой и сжатой зоне, имеют следующий вид [3-6]:
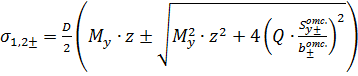 , (4)
, (4)
где D ![]() .
.
Точка, в которой главные напряжения достигают экстремальных значений в произвольном сечении, определяется из условия ![]() = 0 или
= 0 или
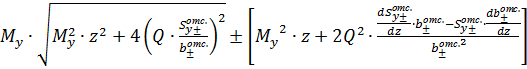 =0
=0
Упростив, получим это выражение в следующем виде:
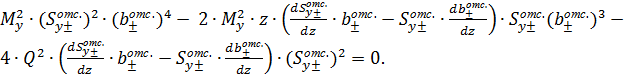
Проводится расчёт на прочность армированных балок с заполнителем из бимодульного материала с использованием теорий прочности [7-8]. Ниже даны формулы расчётных напряжений и условий прочности для различных классических теорий прочности [9] и критериев прочности [10] бимодульных материалов.
1). Теория наибольших нормальных напряжений.
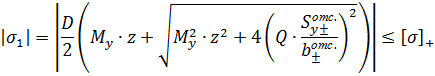
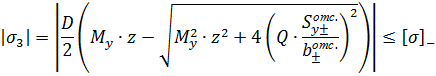
2). Теория наибольших линейных деформаций.
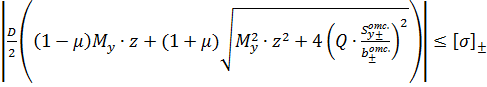 .
.
3).Теория наибольших касательных напряжений.
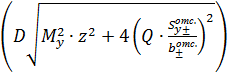
![]() .
.
4). Энергетическая теория прочности.
![]() =
= 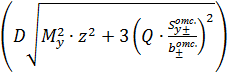
![]()
5). Критерий Шлейхера (K.Schleicher).
![]() +(
+(![]() )
)![]() =
=![]() .
.
Для балки с бимодульным заполнителем критерий Шлейхера имеет вид:
![]() +
+![]()
![]() =
=![]() .
.
Для армированной балки с бимодульным заполнителем критерий Шлейхера имеет вид:
![]() (
(![]() )
) =
![]() .
.
При z =![]() ,
, ![]() ,
, ![]() и получаем критерий Шлейхера для нормальных напряжений:
и получаем критерий Шлейхера для нормальных напряжений:
![]() (
(![]() )
)![]() =
=![]() .
.
При z = 0, ![]() =0 и получаем критерий Шлейхера для касательных напряжений:
=0 и получаем критерий Шлейхера для касательных напряжений: ![]() .
.
6). Критерий П.П. Баландина.
![]() +(
+(![]() )
)![]() =
=![]() .
.
Для балки с бимодульным заполнителем критерий П.П. Баландина имеет вид:![]() (
(![]() )
)![]() =
=![]() .При z =
.При z =![]() ,
, ![]() ,
, ![]() и получаем критерий П.П. Баландина для нормальных напряжений:
и получаем критерий П.П. Баландина для нормальных напряжений:
![]() (
(![]() )
)![]() =
=![]() . При z = 0,
. При z = 0, ![]() =0 и получаем критерий Шлейхера для касательных напряжений:
=0 и получаем критерий Шлейхера для касательных напряжений: ![]() .
.
Здесь ![]() - предел прочности на растяжение,
- предел прочности на растяжение, ![]() - предел прочности на сжатие.
- предел прочности на сжатие.
Литература:
- 1.Амбарцумян С. А. Разномодульная теория упругости.: - М. изд-во” Наука”, Гл. ред. физ.-мат. литературы, 1982.-317 с.
2. Кадомцева Е.Э., Моргун Л.В.. Учёт влияния отличия модулей упругости на сжатие и растяжение при расчёте на прочность армированных балок с заполнителем из фибропенобетона. [Электронный ресурс] // «Инженерный вестник Дона», 2013, № 2. – режим доступа: http://www.ivdon.ru/magazine/archive/n2y2013/1655 (доступ свободный) - Загл. с экрана . - Яз.рус.
3.Андреев В.И., Языев Б.М. Выпучивание продольно сжатых стержней переменной жесткости при ползучести [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4(ч.2.). – режим доступа: http: http://www.ivdon.ru/magazine/archive/n4p2y2012/1259 (доступ свободный) - Загл. с экрана . - Яз.рус.
4. Моргун Л.В., Смирнова П.В., Моргун В.Н., Богатина А.Ю. Конструкционные возможности фибропенобетона неавтоклавного твердения// Ж. «Строительные материалы», 2012, №4. – С.14…16.
5. Филин А.П. Прикладная механика твёрдого деформируемого тела. Т.1. - М. изд-во” Наука”, Гл. ред. физ.-мат. литературы, 1981.-832 с.
6. Кадомцева Е.Э. Прочность при ударе по составной балке. ”Строительство 2009”, Материалы юбилейной международной научно- практической конференции/Ростовский государственный строительный университет - Ростов-на-Дону: редакционно-издательский центр РГСУ, 2009.-228с.
7. Чепурненко А.С., Языев Б.М. Оптимизация формы поперечного сечения сжатых стержней из условия устойчивости//Научное обозрение. 2012. № 6. — С. 45-49.
8. Andreev V.I. The method of optimization of thick-walled shells based on solving inverse problems of the theory of elasticity of inhomogeneous bodies. Computer Aided Optimum Design in Engineering XII. WITpress. 2012. Pp. 189—201.
9. Andreev V., Potekhin I.A. Modeling equally strong cylinder based iterative approach // International Journal for Computational Civil and Structural Engineering, v. 4, is. 1, 2008, p. 79- 84
10. Языев Б.М. Устойчивость жесткого сетчатого полимерного стержня с учетом начальных несовершенств. – М.: Обозрение прикладной и промышленной математики, 2008, Том 15, вып. 2.