Кинематическое исследование механизма поворота ковша канатного экскаватора

Аннотация

Ю.В. Максимов

Дата поступления статьи: 15.12.2013

Проведено кинематическое исследование механизма поворота ковша канатного экскаватора. Рассмотрена часть траектории рабочего процесса, на которой осуществляется поворот рукояти относительно стрелы с одновременным поворотом ковша относительно рукояти. Поворот ковша осуществляется за счет дополнительной кинематической связи ковша с рукоятью и/или стрелой и реализующей внутренние усилия, обусловленные соответствующим взаимным расположением стрелы и рукояти.

Ключевые слова: канатный экскаватор, поворот ковша, кинематика, аналттическое исследование

05.05.04 - Дорожные, строительные и подъемно-транспортные машины

Производственные наблюдения рабочего процесса копания экскаватором ЭО-4112 с обратной лопатой, показали, что главной причиной снижения его эксплуатационной производительности является потеря части зачерпнутого грунта на участке подъема и переноса его к месту выгрузки. Это обусловлено, прежде всего, конструктивными особенностями жесткого крепления ковша к рукояти, при котором положение ковша определяется только двумя угловыми координатами: углами поворота стрелы –  и рукояти – . Это в принципе исключает возможность рационального положения ковша на соответствующем участке траектории (заглубления, зачерпывания, транспортирования, выгрузки). На гидравлических экскаваторах эта проблема решается путем шарнирного соединения ковша с рукоятью и управлением его поворотом дополнительным гидроцилиндром, т.е. положение ковша в этом случае определяется уже тремя координатами – ,  и углом поворота ковша – . Для экскаваторов с канатной подвеской шарнирное крепление ковша к рукояти требует дополнительного устройства управления его поворотом. При этом известные схемы внешнего воздействия на ковш практически невозможно согласовать с существующей конструкцией рабочего оборудования. Решение данного вопроса возможно только за счет дополнительной кинематической связи ковша с рукоятью и/или стрелой и реализующей внутренние усилия, обусловленные соответствующим взаимным расположением стрелы и рукояти [1].
Для практической реализации предложенной конструкции необходимо провести кинематическое и динамическое исследование механизма поворота, схема которого представлена на рисунке.
Схема отражает наиболее значимую в свете рассматриваемого вопроса часть траектории рабочего процесса, на которой осуществляется поворот рукояти относительно стрелы с одновременным поворотом ковша относительно рукояти.
Расположим центр прямоугольной системы координат О₁ в точке крепления рукояти к стреле совместив ось X с линией соединяющей точку поворота рукояти с точкой поворота стрелы О₃. В рассматриваем случае ось Х горизонтальна (угол поворота стрелы ), гидроцилиндр Ц₂ закрыт, т.е. звено АВ жесткое, а гидроцилиндр Ц₁ открыт, что позволяет эвену КН изменять свою длину в соответствии с поворотом ковша.
Механизм поворота ковша представляет собой два смежных четырехзвенных механизма: О₁АВО₂ и О₂СDE, где для первого механизма О₁АВО₂  ведущим звеном является рукоять 1 (звено О₁О₂). Звено 1 вращается с угловой скоростью ω₁ за счет тягового каната 12 наматываемого на барабан главной лебедки с приводом от электродвигателя (Т_дв). Для второго механизма О₂СDE ведущим является звено 5 (О₂С) которое есть продолжение звена 2 (О₂В) первого механизма О₁АВО₂. В результате кинематического анализа должны быть установлены функциональные зависимости углов φ₂, φ₃, φ₅, φ₆и φ₇ обоих четырехзвенных механизмов от ведущего звена 1, а также угловые скорости ω₂, ω₃, и ω₇. Эти зависимости позволят определить угол поворота ковша как по отношению к рукояти 1, так и по отношению к горизонту (линия передней грани боковой стенки ковша 11), а так же скорости перемещения гидроцилиндров Ц1 (тяга переменной длины 10) и Ц2 (тяга переменной длины – звено 3).
Известны различные методы аналитического исследования плоских шарнирных механизмов [2-8] включая и исследование кинематики рабочего органа одноковшового экскаватора [9] и его нагружения [10]. В последнее время для решения задач синтеза все шире используются различные компьютерные программы [5,6]. В известном труде [2] задачи кинематического исследования сводятся к совместному решению уравнений проекций на оси координат контуров, образованных звеньями механизмов, с последующим дифференцированием этих уравнений для определения угловых скоростей. А в [3] первую часть задачи определяют другим способом – путем решения дополнительно построенных на исследуемом механизме треугольников.

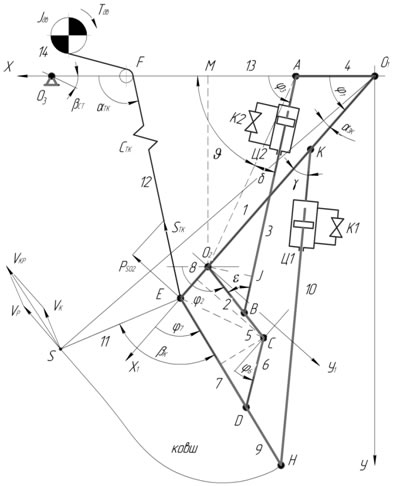
Рис. – Схема механизма поворота ковша

В рассматриваемом механизме соотношения длин звеньев определяют его работу по повороту ковша только в одной четверти окружности, причем проекции звеньев 2 и 3 пересекаются, что выводит данный механизм из ряда классических. Это определило комбинированный подход к решению поставленной задачи.
Обозначим для краткости длины звеньев
O₁O₂ =l₁; O₂B =l₂; AB =l₃; AO₁ =l₄; O₂C =l₅; CD =l₆; ED =l₇; EO₂ =l₈; EH =l₉; HK =l₁₀; EF =l₁₂; O₁F = l₁₃.
Для определения угловой скорости ω₁ звена 1 запишем из треугольника О₁FE векторное равенство
FE = O₁E + FO₁ .
Уравнения проекций на оси координат                     
 (1)
.                                                      
Для определения угла  разделим второе уравнение на первое. Получим
 .
Для определения угловой скорости звена 1 дифференцируем по времени t первое уравнение из (1).
 .
Из углов в этом уравнении вычтем угол  . Тогда имеем
 .
Откуда находим значение ,    (2)
где  – скорость каната, навиваемого на барабан;
– угол образованный канатом 12 и звеном 13.
Скорость каната с учетом полиспастной системы равна
 ,
где ω_дв – угловая скорость двигателя лебедки;
R_б – радиус барабана;
i – передаточное число привода барабана;
a_п – кратность полиспаста.
Рассмотрим четырехзвенный механизм О₁АВО₂ .
Из прямоугольного треугольника AO₂J следует
    (3)

    (3)

Неизвестные углы φ₃ и ε определяются из соответствующих треугольников, построенных на исследуемом механизме.
Из прямоугольного треугольника АО₂М получаем
,       (4)

а из треугольников О₁О₂А  и  О₂АВ

 .

Откуда   .
Обозначим
  и   . (5)
Окончательно имеем                                                 
Таким образом, вычисляя последовательно по формулам (5), (4) и (3) углы ε, v и δ, определяем угол
 .    (6)

Для определения угла φ₂ и скоростей звеньев механизма воспользуемся методом, изложенным в [2].
Векторное уравнение замкнутости контуров О₁АВО₂
 .
Проектируя это уравнение на оси O₁X и O₁Y, получаем
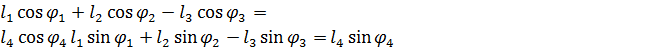(7). 

Так как , то   и  , то уравнения (7) получают вид

 .      (8)

Угол φ2 определяется из последнего уравнения (8)
 .    (9)                                              
Для определения угловых скоростей ω₂ и  ω₃ звеньев 2 и 3 дифференцируем уравнения (8) по времени t . Получаем
 
 .
Имея в виду, что    ,    и   , имеем
 .    (10)
                                
Из углов входящих в первое уравнение (10) вычитаем общий угол φ₂ , что соответствует повороту осей координат XO₁Y  на угол φ₂ . Получаем
 ,
Откуда находим угловую скорость звена 3
 . (11)                                                     
После аналогичного преобразования первого уравнения (10) путем поворота осей координат XO₁Y на угол φ₃ получаем выражение для угловой скорости
 .  (12)
 Для определения угла непосредственно характеризующего поворот ковша (звено 7) относительно рукояти (звена 1) рассмотрим смежный четырехзвенный механизм O₂CDE. Введем подвижную систему координат X₁O₂Y₁, связав её с центром вращения ведущего (для смежного механизма) звена O₂C. Обозначив дополнительные углы O₂EC = v₂ , O₂EC = δ₂ и O₂EC = и выполнив все аналогичные вышеприведенным для механизма О₁АВО₂ преобразования в результате получаем выражения для определения всех значимых углов и угловых скоростей. ;  ;
,
где  ;    .
  (13)
  (14)
 .(15)
Скорость изменения длины звена 10 (хода поршня гидроцилиндра Ц1)
определяется из векторного уравнения
КЕ + ЕН = НК .
Уравнения проекций этого уравнения на оси координат имеют вид

.  (16)
Разделив второе уравнение на первое, получаем значение угла
 (17)
Для определения скоростей продифференцируем по времени t уравнения (16). Получаем

 .   (18)
Из углов в уравнениях (18) вычитаем угол . В результате получаем значения скоростей.
Скорость изменения длины звена 10 () равна
.  (19)
Угловая скорость звена 10
.
Полученные функциональные зависимости кинематических параметров механизма поворота одноковшового экскаватора в виде выражений (1)…(19) позволяют проводить анализ механизма для любых значений угла поворота рукояти .

Литература:

1. Патент РФ 2450106, МПК Е02F 3/42. Рабочее оборудование ковшового экскаватора / В.С. Исаков, Ю.В. Максимов, Г.М. Симелейский; заявлено 15.10.2010; опубл. 10.05.2012, Бюл. № 13. – 8 с., ил.
2. Артоболевский И.И. Теория механизмов и машин. [Текст]. Издание третье. – М.: Гос. изд-во технико-теоретической литературы, 1953. – 712 с.
3. Кожевников С.Н. Теория механизмов и машин. [Текст]. – М.: Машгиз, 1949. – 448 с.
4. Зиновьев В.А. Аналитические методы расчета плоских механизмов. [Текст]. М., Гостехиздат, 1949. – 204 с.
5. Зиборов К.А. Решение векторных уравнений кинематики механизмов с помощью программы Mathcad [Текст] / К.А. Зиборов, И.Н. Мацюк, Э.М. Шляхов // Теория механизмов и машин. 2008. №1. Том 6. С. 64-70.
6. Верховод  П.В. Решение задачи приближенного синтеза четырехзвенного механизма с помощью программы mathcad [Текст] // Теория машин и механизмов. – 2011. – № 2, Том 9. – С. 53-64.
7. Hartenberg, R.S., and Danavit, J. 1964, Kinematic Synthesis of Linkages. McGrawHill, Ney York. http://ebooks.library.cornell.edu/cgi/t/text/text-idx?c=kmoddl;idno=kmod013.
8. Freudenstein, F. Approximate synthesis of four-bar linkages. Transactions of ASME, 1955, Vjl. 77, pp. 853-861/
9. Павлов В.П. Информационно-логическая модель системного проектирования одноковшовых экскаваторов [Электронный ресурс] // Инженерный вестник Дона, 2010. №3. – Режим доступа: htt: // www/ ivdon.ru / magazine / archive/n3y2010/238 / (доступ свободный). – Загл. с экрана. – Яз. рус.
10. А.А. Котесова. Уточненное определение ресурса совокупности по выборочным данным для стрелы одноковшового экскаватора [Электронный ресурс] // Инженерный вестник Дона, 2013. №2. – Режим доступа: htt: // www/ ivdon.ru / magazine / archive / n2y2013/1695 / (доступ свободный). – Загл. с экрана. – Яз. рус.