К вопросу определения релаксационных констант уравнения связи максвелла для жестких полимеров в задачах устойчивости

Аннотация

И.И. Кулинич, С.Б. Языев, С.Б. Языева

В статье показано, что вязкоупругое  поведение полимеров хорошо описывается нелинейным обобщенным уравнением Максвелла, обобщенным  российским ученым Г.И. Гуревичем
В данной работе на основе результатов экспериментальных исследований изотермической релаксации температурных напряжений представлен метод определения релаксационных параметров уравнения (1). Эксперимент проводился на тонкостенных трубках, с жестко защемленными торцами. Нагревание или охлаждение от начальной температуры  до конечной температуры  (температуры релаксации) осуществлялось с постоянной скоростью нагревания (охлаждения)  по линейному закону. Данная работа показывает, что линеаризованная теория  не дает верных результатов. Ключевые слова: Температурные напряжения, параметры уравнения связи Максвелла,  изотермическая релаксация.

Ключевые слова: Температурные напряжения, параметры уравнения связи Максвелла, изотермическая релаксация

05.23.17 - Строительная механика

Во многих работах [1-5 и др.] показано, что вязкоупругое  поведение полимеров хорошо описывается нелинейным обобщенным уравнением Максвелла, сформулированным российским ученым Г.И. Гуревичем. Для одномерного случая  нагружения  это уравнение имеет вид:

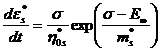(1)

 где- s-тая составляющая спектра высокоэластической деформации, - начальная релаксационная вязкость, - модуль высокоэластичности, - модуль скорости деформации.
В данной работе на основе результатов экспериментальных исследований изотермической релаксации температурных напряжений представлен метод определения релаксационных констант уравнения (1).
В качестве объекта исследования рассматривались: полиметилметакрилат, имеющий линейную структуру, и эпоксидная смола ЭДТ-10, имеющую сетчатую структуру. Эксперимент проводился на тонкостенных трубках, с жестко защемленными торцами. Нагревание или охлаждение от начальной температуры  до конечной температуры  (температуры релаксации) осуществлялось с постоянной скоростью нагревания (охлаждения) по линейному закону:

  В момент времени  в образце достигалась температура  и напряжения , которые были начальными для процесса изотермической релаксации температурных напряжений.
Если  (нагревание), напряжения со временем уменьшались и через определенное время стремились к горизонтальной асимптоте, соответствующей напряжению .
Как показывает эксперимент, конечные напряжения  в процессе изотермической релаксации температурных напряжений не зависят от скорости нагревания  (охлаждения)  и, таким образом, от начальных напряжений . Но напряжения  зависят от температуры релаксации  и температурного перепада . Эта зависимость для обоих полимеров может быть записана в виде:

Таким образом, из этой экспериментальной зависимости мы можем найти .  Введем абсолютный и относительный перепады напряжений  и . Тогда из экспериментальных кривых  мы можем вывести кривую зависимость 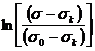 как функцию времени . Из этих кривых можно заметить, что они после некоторого времени становятся прямыми линиями, и можно написать:

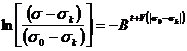
Таким образом,  мы можем получить константы  и .
Ниже показано, что три эмпирических константы  имеют теоретические аналоги из обобщенного уравнения Максвелла, если мы рассматриваем только одну составляющую вязкоупругой деформации.
Положим, что полная деформация  является суммой:

(3)

   Здесь  - упругая деформация; -высокоэластическая деформация, 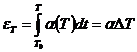- температурная деформация.
Поскольку торцы образца защемлены, можно положить  и при определенной температуре . Тогда из (1) и (3) получим:

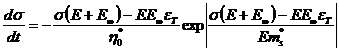(4)

Принимая во внимание, что в конце изотермической релаксации температурных напряжений , из (4) мы можем получить

Этот результат соответствует (2), и мы имеем

Таким же образом мы можем получить формулы для констант  и .

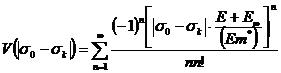
 Если в (1) формально заменить экспоненту единицей, то получим линейную (или линеаризованную) теорию. Нетрудно показать, что линейная теория дает другие результаты и не позволяет описать процесс изотермическую релаксацию температурных напряжений.

Выводы
Таким образом, если в (1) формально заменить экспоненту единицей, то получим линейную (или линеаризованную) теорию. Нетрудно показать, что линейная теория дает другие результаты и не позволяет описать процесс изотермической  релаксации температурных напряжений.

Литература

1.Андреев В.А.  Некоторые задачи и методы механики неоднородных тел. М.: АСВ, 2002.- 288 с.
2.Турусов Р.А.  Механические явления в полимерах и композитах. Докт. дисс., М., 1983. – 363 с.
3.Рабинович А.Л. Введение в механику армированных полимеров, - М.:       «Наука», 1970.- 482 с.
4.Гуревич Г.И. Деформируемость сред и распространение сейсмических волн. –М.: Наука, 1974.- 482с.
5.Языев Б.М. Устойчивость жесткого сетчатого полимерного стержня с учетом начальных несовершенств. – М.: Обозрение прикладной и промышленной математики, 2008,  Том 15, вып. 2.
6.Самарский А.А., Андреев В.Б. Разностные методы для эллиптических уравнений. - М.: Наука,  1976. - 352 с.
7.Аскадский А.А. Деформация полимеров. – М.: Химия, 1973. - 448 с.